내력벽식 스터드패널을 적용한 모듈러건물유닛의 내진성능

1. 서  론

최근 학교, 군병영시설, 도심형생활주택 등 동일한 단위평면이 반복되는 저층건물을 중심으로 모듈러공법의 적용이 점차 늘어나는 추세이다. Fig. 1에 나타낸 바와 같이 모듈러공법은 규격화된 건물모듈 유닛을 공장에서 제작한 다음 현장에 반입하여 단순 조립하는 공법으로, 현장공정을 최소화를 통하여 공기단축, 비용절감, 중량감소, 높은 수준의 공사품질 확보 등의 장점을 확보할 수 있다. 하지만 일반적으로 단위모듈 또는 단위모듈 사이의 접합부 등에서 내진성능을 확보하는 것이 쉽지 않다. 따라서 단위모듈은 중력하중에만 저항하고 지진하중은 별도의 코어벽 또는 가새구조으로 저항하는 방법이 사용되기도 한다[1]. 그러나 모듈러공법의 경제성을 높이기 위해서는 중력하중과 횡하중에 동시에 저항할 수 있는 단위모듈을 사용하는 것이 더 유리하다.

단위모듈의 중력하중 및 횡하중에 대한 저항성능을 확보할 수 있는 방안으로 가새골조모듈(Framed module with diagonal bracing), 이중강판패널 보강 골조모듈(framed module with double skin steel panels), 스터드패널 보강 모듈러시스템(modular system with stud panels, Fig. 1 참조) 등이 개발되었다[2],[3],[4],[5],[6],[7],[8],[9]. 이 중 Fig. 1에 나타낸 스터드패널 모듈러시스템은 용접 및 강재물량을 절감하는데 가장 효과적이다[4],[5],[6],[7],[8],[9]. 또한, 냉강성형형강 부재는 가공성이 탁월하기 때문에 단면의 형상을 사용 목적에 따라 다양화하여 사용할 수 있는 장점이 있다[10]. 스터드패널은 수직방향으로 배치되는 스터드(stud, 경량 ㄷ형강 또는 ㅁ형강)가 중력하중에 저항하고, 대각방향으로 설치된 스트랩브레이스(strap brace)는 횡하중에 저항한다. 각 스터드패널은 단위모듈 내에서 다이아프램 거동을 보이도록 상･하부 콘크리트 슬래브 및 테두리보에 의하여 강하게 연결된다.

본 연구에서는 스터드패널과 경량철골골조로 구성된 모듈러건물 유닛의 강성, 하중재하능력, 연성능력, 에너지소산능력, 파괴모드 등 내진성능을 평가하기 위한 주기실험을 수행하였다. 모듈러건물 유닛의 횡력저항요소로서 스트랩브레이스 및 시트강판으로 보강된 스터드패널을 적용하였다. 소성메커니즘을 근거로 모듈러건물 유닛의 강도, 항복변위, 탄성강성 등 설계식을 제안하였고 실험결과와 비교를 통하여 제안된 설계식을 검증하였다.

2. 스터드패널의 횡력저항

2.1 스트랩 스터드패널

모듈러건물유닛은 경량형강 테두리골조와 골조 내부의 스터드패널로 구성된다(Fig. 1 참조). Fig. 2(a)는 모듈러건물 유닛 내부에서 삽입되는 스트랩브레이스 보강 스터드패널(strap-braced stud panel, 이하 스트랩스터드패널)의 형상 및 상세를 보여준다. Fig. 2(a)에 나타낸 바와 같이, 스트랩브레이스의 횡력은 스터드패널 각 모서리에서 스크류볼트 접합(screw bolting)을 통하여 거셋플레이트(gusset plates)로 전달되고, 다시 연결강판(connector plates)을 통하여 테두리골조의 상ㆍ하 보로 전달된다. 스터드패널과 테두리골조 사이의 명확한 하중전달을 위하여, 연결강판은 스터드패널의 거셋플레이트에 스크류볼트로 이음되고 완전용입 구조용접(CJP structural welding)으로 테두리골조의 상ㆍ하 보에 접합된다.

Fig. 2(b)는 스트랩스터드패널의 소성메커니즘을 보여준다. 기존연구[4],[5],[6],[9]에 따르면, 스크류볼트 접합부의 취성파괴가 조기에 발생하지 않는 경우 스트랩스터드패널은 항복이후 우수한 연성거동을 보인다. 박판의 스트랩은 압축에 대하여 전혀 저항하지 못하므로 스터드패널은 오직 스트랩브레이스의 인장작용에 의해서만 횡력에 저항하고, 따라서 스터드패널의 소성메커니즘은 Fig. 2(b)에 나타낸 바와 같이 스트랩브레이스의 인장항복으로 단순화시킬 수 있다. 이러한 소성메커니즘을 바탕으로 모듈러건물유닛의 공칭강도 , 항복변위 , 탄성강성 은 다음과 같이 쉽게 계산할 수 있다.

 (1)

 (2)

 (3)

여기서, = 모듈러건물 유닛에 포함된 스터드패널의 개수, 및 = 각각 스트랩브레이스의 항복응력 및 항복변형률, = 스트랩브레이스의 단면적, = 인장항복하는 스트랩브레이스의 길이(Fig. 2(a) 참조), = 수평축에 대한 스트랩브레이스의 경사각이다.

Fig. 2(a)에 나타난 바와 같이 박판의 스트랩브레이스는 스크류볼트를 사용하여 스터드패널 네 모서리에서 거싯플레이트와 연결된다. 스크류볼트 접합부의 공칭저항 은 스트랩 지압파괴, 스트랩 순단면파단, 스크류볼트 전단파단 등을 고려하여 다음과 같이 계산한다[11],[12].

 (4)

 (5)

 (6)

여기서, = 스트랩브레이스의 지압파괴강도, = 스트랩브레이스의 두께, = 강판 두께의 영향을 고려하는 강도보정계수[11],[12], = 스트랩브레이스의 극한강도, = 스크류볼트 직경, = 스트랩브레이스의 순단면파단강도, = 스트랩브레이스의 순단면적, = 스크류볼트의 전단강도, = 스크류볼트 항복응력, = 스크류볼트 단면적이다. 스트랩브레이스 접합부의 공칭강도 은 식 (4)∼(6) 중 가장 작은 값으로 결정된다.

Fig. 2(a)와 나타낸 바와 같이 수평스트럿(horizontal strut), 스터드, 스트랩브레이스 등이 모이는 스터드패널의 모서리에서는 스트랩브레이스가 전달하는 대각방향 인장력의 수직분력을 스터드가 저항하여야 한다. 즉, 스터드에 작용하는 압축력 는 스터드패널 모서리에서의 하중평형조건으로부터 결정되어야 한다. 극한한계상태에서 스트랩브레이스가 인장항복하는 것으로 가정하면, 스터드에 작용하는 압축력 는 다음과 같이 계산할 수 있다.

 (7)

여기서, = 중력하중에 의하여 스터드에 작용하는 압축력이다. Fig. 2(a)의 예시된 스트랩스터드패널의 경우 총 4개의 수직방향 스터드를 사용하고 있지만, 오직 두 개의 외부 스터드에만 스트랩브레이스의 횡력저항에 의한 추가적인 압축력(즉, )이 발생된다. 내부 스터드는 중력하중에 의한 압축력(즉, )에만 저항하도록 설계한다.

2.2 시트강판 스터드패널

Fig. 3은 본 연구에서 제안하는 시트강판 보강 스터드패널(sheeted stud panel, 이하 시트강판스터드패널)의 형상 및 상세를 보여준다. Fig. 1에 예시된 바와 같이, 하나의 모듈러건물유닛 내부에 여러 개의 시트스터드패널이 테두리골조에 의하여 강하게 묶여 다이아프램거동을 나타낸다. Fig. 3에 나타낸 바와 같이, 얇은 두께의 시트강판은 스터드패널의 네 모서리에서 스크류볼트 접합을 통하여 연결강판(connector plate)과 접합된다. 특히, 시트강판과 스터드패널의 접합은 오직 네 모서리의 연결강판에 의해서만 이루어지므로, 시트강판스터드패널은 등가의 스트랩브레이스로 보강된 스터드패널로 이상화할 수 있다. 등가 스트랩브레이스의 폭과 길이를 각각 및 로 가정할 경우, 시트강판스터드패널의 횡력저항강도 , 항복변위 , 탄성강성 은 다음과 같다.

 (8)

 (9)

 (10)

여기서, 및 =각각 시트강판의 항복응력 및 항복변형률, 및 =각각 등가 스트랩브레이스의 단면적과 길이, =강판 두께, =수평축에 대한 등가 스트랩브레이스의 경사각이다.

Fig. 3에 나타낸 바와 같이, 시트강판(또는 등가 스트랩브레이스)이 저항하는 횡하중은 스크류볼트 접합부를 통하여 연결강판으로 전달되고, 최종적으로 테두리골조의 상ㆍ하 보로 전달된다. 이러한 횡하중 전달을 명확하게 하기 위하여, 연결강판과 테두리보는 구조용접으로 접합된다. 또한 연결강판과 시트강판을 연결하는 스크류볼트는 등가 스트랩브레이스의 방향과 일치하도록 대각방향으로 배열한다. 연결강판와 패널강판의 접합에 필요한 스크류볼트 소요개수는 등가 스트랩브레이스의 전단면 항복에 의한 인장력(= )에 저항하도록 결정한다. 연결강판과 패널강판 사이 스크류볼트 접합부의 공칭저항강도는 폭 의 스트랩브레이스로 간주하여 식 (4)～(6)을 사용하여 계산한다.

3. 실험 계획

Fig. 4는 스트랩스터드패널을 사용한 모듈러건물유닛 실험체 SDS의 상세도면을 보여준다. SDS실험체는 경량형강의 테두리골조와 내부에 삽임된 4개의 스트랩스터드패널로 구성된다. 좌･우 기둥 중심거리와 상･하 보 중심 높이(층고 )는 각각 5,713mm 및 3,000mm이다. 기둥과 보는 각각 ㄷ-130×110×4.5 및 ㄷ-130×110×6의 경량형강을 사용하였다. 테두리골조의 보-기둥 접합부는 원칙적으로 모듈러건물유닛의 횡력저항에 기여하지 않는 핀접합이지만, 실제 테두리골조의 보-기둥 접합부는 용접접합으로 제작하였고 4.5mm 두께의 다이아프램 강판으로 보-기둥 조인트를 보강하였다. 반복재하 실험을 위한 가력보(loading beam) 및 바닥지그(bottom jig)로서 경량형강 ㄷ-130×110×6을 사용하였다. 가력보와 바닥지그는 8개의 M24 일반볼팅으로 테두리골조의 상･하 보에 단순고정하였다.

Fig. 5는 SDS에 사용된 스트랩스터드패널 상세를 보여준다. 스터드패널의 수직높이와 수평길이는 각각 2,868mm 및 1,388mm이다. 상･하 수평스트럿(horizontal strut)은 ㄷ-104×40×1.6을 사용하였고, 스터드의 면내방향 횡지지를 위하여 중간 높이에 PL-80×1.0 (너비 80mm, 두께 1.0mm의 강판)의 타이 스트랩(tie strap)을 설치하였다(Fig. 5의 Detail A 참조)[13]. 외측 스터드(stud 1)는 ㅁ-100×50× 1.2 형강을 사용하였고, 내측 스터드(stud 2)는 플랜지 단부가 절곡된 ㄷ-100×40×12×1.2 형강을 사용하였다(Fig. 5의 단면형상 참조). Fig. 2(a) 및 식 (7)에 나타낸 바와 같이 외측 스터드는 스트랩브레이스의 인장력에 의하여 압축력이 추가로 재하되므로, 좌굴에 대한 저항성이 높은 사각형 단면을 사용하였다. 스터드패널의 스터드, 수평스트럿, 타이 스트랩 사이의 접합은 스크류볼트( 5.5mm)를 사용하였다. 대각방향으로 설치되는 스트랩브레이스는 PL-125×1.0(너비 125mm, 두께 1.0mm의 강판)을 사용하였다( = 2630mm 및 = 64°). Fig. 5의 Detail B는 스터드패널 모서리에서 스트랩브레이스, 거셋플레이트, 스터드, 수평스트럿 사이의 접합상세를 보여준다. 거셋플레이트 PL-300×250×1.6(높이 300mm, 너비 250mm, 두께 1.6mm의 강판)을 스크류볼트( 5.5mm)를 사용하여 스터드(9개)와 수평스트럿(6개)에 고정한 다음, 스트랩브레이스를 거셋플레이트에 스크류볼팅(18개, 5.5mm)으로 접합하였다.

Fig. 4는 스트랩스터드패널을 테두리골조에 접합하기 위하여 사용한 4.5mm 두께의 연결강판 CP1 및 CP2의 상세를 보여준다. 연결강판 CP1 및 CP2는 18개의 스크류볼트( 5.5mm)를 사용하여 거싯플레이트와 이음하였고(Fig. 5의 Detail B 참조), 다음으로 테두리골조의 상ㆍ하 보에 구조용접으로 접합되었다. 테두리골조의 상ㆍ하 보는 4.5mm 두께의 스티프너(stiffener, Fig. 4 참조)를 사용하여 용접부를 보강하였다. 테두리골조의 좌ㆍ우 기둥과 스터드패널의 스터드는 일반볼트 M24로 단순 고정하였다(Fig. 4의 CP1 상세 참조).

Fig. 6은 0.4mm 두께의 얇은 시트강판으로 보강한 시트강판스터드패널을 사용하는 모듈러건물유닛 실험체 SSP의 상세 도면을 보여준다. 테두리골조, 가력보(loading beam), 바닥지그(bottom jig)의 단면크기와 상세는 SDS 실험체와 동일한다. 비록 테두리골조의 보-기둥 접합부는 횡력저항에 기여하지 않는 핀접합으로 설계되지만, 본 실험에서는 보-기둥 접합부를 용접으로 제작하였고 4.5mm 두께의 다이아프램 강판으로 접합부를 보강하였다.

테두리골조 내부에는 2,686mm×1,388mm 크기의 강판스터드패널 4개를 설치하였다. Fig. 5의 SDS 실험체의 스트랩스터드패널과 동일하게, 스터드패널의 상･하 수평스트럿과 중간의 타이스트랩은 각각 ㄷ-104×40×1.6 및 PL-80× 1.0을 사용하였고, 외측 및 내측의 스터드는 각각 ㅁ-100× 50×1.2 및 ㄷ-100×40×12×1.2를 사용하였다. 스터드패널에 클래딩된 시트강판 PL-2686×1388×0.4(높이 1,686mm, 너비 1,388mm, 두께 0.4mm의 시트강판)은 180mm 간격의 스크류볼트( 5.5mm)를 사용하여 각형단면의 외측 스터드(stud 1, Fig. 5 참조)와 상･하 수평스트럿에 고정하였다(Fig. 6 Detail A 참조). 하지만 내부 스터드(stud 2, Fig. 5 참조)에는 시트강판을 스크류볼트로 고정하지 않았다. 시트강판의 클래딩을 위한 외부스터드 및 수평스트럿의 스크류볼트는 구조계산에서 제외하였다.

Fig. 6은 시트강판스터드패널과 테두리골조를 접합하는 연결강판 CP3 및 CP4의 상세를 보여준다. CP3 및 CP4은 각각 4.5mm 두께의 L형 및 T형 단면을 갖는다. 스터드패널의 모서리마다 연결강판 CP3 및 CP4는 대각방향으로 배열된 22개의 스크류볼트( 5.5mm, 간격 50mm)를 사용하여 0.4mm 두께의 시트강판에 이음되었다( =300mm, =2,430mm, = 70°). 그 다음 CP3 및 CP4는 테두리골조의 상ㆍ하 보에 구조용접으로 접합되었다. 용접 접합부 근처는 4.5mm 두께의 스티프너(stiffener)를 사용하여 테두리골조의 상ㆍ하 보를 보강하였다.

Table 1은 실험에 사용된 강판 및 경량형강에 대하여 인장시험으로부터 구한 항복강도 및 인장강도를 보여준다. 모든 강판 및 형강의 재질은 SS400이다. 항복 및 인장강도는 시편 3개로부터 구한 값의 평균을 나타낸다. Table 1에 나타낸 바와 같이, 모든 강판 및 형강의 항복강도는 SS400 강재의 설계항복강도 235MPa보다 컸다. 그러나 1.6mm 두께의 거셋플레이트와 테두리 기둥 및 보의 경향형강 시험편에서 계측한 인장강도는 SS400 강재의 공칭인장강도 400MPa보다 작았다. 스크류볼트( 5.5mm) 및 M24 볼트 또한 SS400 강재로 제작되었다. 실험체 제작에 사용된 용접법은 플럭스코어드아크용접(Flux-Cored Arc Welding)으로 용접금속의 인장강도는 FEXX=550MPa이다.

Fig. 7은 SSP 실험체의 가력을 위한 실험체 셋팅 사진을 보여준다. 500kN 엑츄에이터(최대 스트로크 ±190mm)를 가력보(loading beam)에 연결하여 횡하중을 반복가력하였다. 엑츄에이터의 면외방향 변위를 막기 위하여, Fig. 7에 나타낸 바와 같이 가력보의 두 곳에서 횡지지하였다. 실험은 엑츄에이터의 정･부 방향 횡변위 ±12mm, ±16mm, ±24mm, ±32mm에서 각각 5회 반복가력하였고, 이후 ±48mm, ±64mm, ±96mm, ±128mm, ±160mm, ±180mm 횡변위에서 각각 3회 반복가력하였다. 주기실험 동안 일축 소성변형률게이지를 대각방향으로 스트랩브레이스 및 시트강판에 부착하여 변형률을 계측하였다. 또한 하중-변위 관계의 보정을 위하여 실험체의 바닥지그에 LVDT를 설치하여 미끄러짐을 계측하였다.

4. 실험 결과

4.1 하중-변위 관계 및 파괴 양상

Fig. 8(a)와 (b)는 각각 스트랩스터드패널을 사용한 모듈러건물유닛 실험체 SDS와 시트강판스터드패널을 사용한 모듈러건물유닛 실험체 SSP의 하중-변위 관계를 보여준다. 각 실험체의 주요 파괴양상은 Fig. 9와 10에 나타냈다. 스트랩브레이스는 두께가 얇은 박판이므로, 거셋플레이트에 고정시켜 스터드패널에 붙이더라도 팽팽하지 않고 표면에 굴곡이 발생되었다. 그럼에도 불구하고 항복이전의 초기탄성재하 동안 슬립변형이 발생하지 않았다. Fig. 8(a)의 하중-변위 관계에 나타난 바와 같이, 횡변위 ±16mm에서 SDS의 강성이 감소하기 시작하였고, 횡변위 ±24mm에서 완전히 항복하였다. 횡변위 +32mm 및 -48mm에서는 경량형강으로 제작된 테두리골조의 보-기둥 접합부에서 기둥 다이아프램 용접부 파단이 발생하여 하중재하능력이 저하되었다(Fig. 9의 Detail A 참조). 이러한 기둥 다이아프램 용접부 파단은 스트랩브레이스의 횡력저항으로 인하여 테두리골조의 보-기둥 접합부에 수직 인발력이 작용하였기 때문이다(Fig. 9의 Detail A에 나타낸 Pull of strap brace 참조). 그러나 SDS 실험체의 테두리골조 기둥-보 접합부는 본래 횡하중에 저항하지 않는 핀접합으로 설계되었으므로, 접합부의 기둥 다이아프램 용접부 파괴 이후에도 보강없이 실험을 계속하였다. 횡변위 ±180mm까지 SDS 실험체는 뚜렷한 강도저하 및 강성저하 없이 안정적인 비탄성 주기거동을 보였다. 최종적으로 엑츄에이터 스트로크 제한으로 인하여 횡변위 ±180mm에서 실험을 종료하였다.

Fig. 9는 스트랩스터드패널을 사용한 SDS 실험체의 변형 및 파괴양상을 보여준다. 대각 인장응력장(tension field action) 방향과 동일한 방향의 스트랩브레이스는 팽팽한 상태로 횡하중을 전달하는 반면, 반대방향의 스트랩브레이스는 작은 압축력에도 좌굴이 발생하여 횡하중에 전혀 저항하지 못하였다. 스트랩브레이스는 비탄성 주기거동 동안 인장파단 없이 큰 소성인장변형률을 경험하였다. 하지만 거셋플레이트-스트랩브레이스 또는 거셋플레이트-연결강판 사이의 스크류볼트 접합부는 어떠한 파괴도 발생되지 않았다. 또한 스터드패널 모서리에서 스트랩브레이스 인장력의 수직분력을 저항하는 외측 스터드(ㅁ-100×50×1.6)에도 압축항복 및 좌굴이 전혀 발생하지 않았다(Fig. 8 참조). 엑츄에이터를 밀어내며 가력하는 정방향 재하 동안 가력보에는 면외방향 변위가 조금 발생하였지만, 하중재하능력에는 거의 영향을 주지 않았다.

Fig. 8(b)와 Fig. 10은 시트강판스터드패널을 사용한 모듈러건물유닛 실험체 SSP의 하중-변위 관계와 파괴양상을 각각 보여준다. 스터드패널에 클래딩된 시트강판이 완벽하게 팽팽하게 시공되지는 못하였지만, 초기탄성재하 동안 슬립변형이 전혀 발생하지 않았다. SSP의 경우 비록 공칭 하중재하능력은 스트랩스터드패널을 사용한 SDS 실험체와 조금 작도록 설계되었지만, 시트강판의 잉여저항(redundancy)에 의하여 SDS보다 훨씬 큰 탄성강성을 보였. 횡변위 -16mm에서 테두리골조의 보-기둥 접합부에서 기둥 다이아프램 용접부 파단이 발생되어 강성이 감소하였다(Fig. 10의 Detail A 참조). 테두리골조의 기둥-보 접합부는 횡하중에 저항하지 않는 핀접합부로 설계되었으므로, 접합부의 기둥 다이아프램 용접부 파괴에도 불구하고 보강없이 실험을 계속하였다. 횡변위 +32mm로 엑츄에이터를 밀어내는 정방향 재하 동안에 가력보에 면외방향 변위가 크게 발생하여 SSP의 하중재하능력이 급격히 감소하였다(Fig. 10의 Out-of-plane displacement of loading beam 참조). 따라서 이후에는 엑츄에이터를 당기는 부방향으로만 주기실험을 수행하였다.

Fig. 10은 시트강판스터드패널의 변형 양상을 보여준다. 대각방향의 인장응력장작용(tension field action)이 일어난 방향으로는 시트강판이 팽팽하게 당겨져 횡하중에 저항하는 반면, 압축이 발생되는 반대방향으로는 강판 좌굴이 크게 발생하였다. Fig. 10의 Detail B에 나타난 바와 같이, 횡변위 -96mm를 초과하면서 연결강판 CP3 및 CP4와 시트강판 사이의 스크류볼트 접합부에서의 시트강판의 지압파괴와 스크류볼트 전단파괴가 발생하였다. 그 결과, SSP의 하중재하능력이 조금 감소하였다. 이러한 스크류볼트 접합부의 파괴에도 불구하고, 시트강판을 스터드패널에 클래딩하기 위하여 사용한 비구조용 스크류볼트(Fig. 6의 Detail A 참조)가 강판의 횡력저항에 추가적으로 기여하므로, SSP실험체는 이후 -160mm까지 하중재하능력을 유지하며 연성거동을 보였다. 최종적으로 테두리골조 보-기둥 접합부에서 기둥의 수직 인발변형(Fig. 10 Detail A의 gap)이 지나치게 증가하여 횡변위 -160mm에서 실험을 종료하였다.

횡변위 -96mm 이후에는 시트강판을 스터드에 클래딩을 위하여 사용한 비구조용 스크류볼트 접합(Fig. 6의 Detail A 참조)으로 인하여 스터드에 의도하지 않은 면내방향의 횡변위가 발생하였다(Fig. 10의 In-plane lateral displacement of stud 참조). 면내방향 횡변위는 스터드의 좌굴저항능력을 저하시킬 수 있다. 실제 모듈러건물에서는 스터드패널은 횡하중 뿐만 아니라 중력하중에도 저항하는 내력벽시스템이므로, 스터드의 횡변위는 스터드패널의 수직하중 저항능력을 저하시킬 우려가 높다. 따라서 시트강판 클래딩을 위한 비구조용 스크류볼트는 최소화시키는 것이 바람직하다. 또한 스터드의 면내방향 횡변위를 막기 위하여 추가적인 횡지지를 제공하는 것이 바람직하다.

4.2 실험결과 분석

Table 2는 실험에 의한 최대강도 , 최대변위 (실험 종료 횡변위), 최대변위비 (= / ), 항복강도 , 항복변위 , 항복변위비 (= / ), 변위연성도 (= / ), 탄성강성 등을 보여준다( =3,000mm). 각 모듈러시스템 실험체의 탄성강성 는 스트랩브레이스와 시트강판의 인장항복이 시작된 횡변위 ±16mm에서의 할선강성을 사용하였고, 항복변위 는 최대강도 를 탄성강성 로 나누어 계산하였다. Table 2는 정방향 및 부방향 재하를 구분하여 나타냈다.

Table 2에 나타난 바와 같이 SDS 및 SSP 실험체 모두 구조체 및 가력방법이 정확히 대칭이므로, 정･부 방향의 최대강도와 탄성강성이 거의 동일하게 나타났다. 2장에 나타낸 설계식을 바탕으로 SDS가 SSP보다 더 큰 공칭강도를 갖도록 설계되었음에도 불구하고, 시트강판스터드패널을 사용한 SSP실험체의 최대강도와 탄성강성은 스트랩스터드패널을 사용한 SDS 실험체 대비 각각 15% 및 44% 컸다. 그 이유는 시트강판을 스터드패널에 클래딩하기 위하여 사용한 비구조용 스크류볼트(Fig. 6의 Detail A 참조)로 인하여 시트강판스터드패널의 횡력저항성능이 등가스트랩브레이스 모델에 의한 공칭값보다 증가하였기 때문이다.

Table 2는 각 실험체의 항복 및 최대변위와 변위연성도를 보여준다. SSP실험체의 최대강도 가 SDS의 최대강도보다 약 15% 크지만 탄성강성 는 44%가 증가하였다. 그 결과 최대강도를 탄성강성으로 나누어 계산한 항복변위 는 SSP가 SDS보다 16～24% 감소하였다. Fig. 8의 하중-변위 관계에 보는 바와 같이, SDS와 SSP 실험체는 5% 이상의 횡변위비에서도 하중재하능력이 크게 저하되지 않았다(면외방향 변위가 발생하여 재하를 포기한 SSP의 정방향 재하 제외). 실험이 종료된 시점의 최대변위비는 = 5.37%∼5.90%이고, 최대변위를 항복변위로 나눈 변위연성도는 = 5.76∼7.60으로 매우 큰 값을 나타냈다. 이러한 최대변위비와 변위연성도는 스트랩브레이스와 시트강판으로 보강한 스터드패널을 사용하는 모듈러건물이 기본적으로 연성구조시스템임을 가리킨다. 하지만, Fig. 8의 하중-변위 관계에 보는 바와 같이, 스터드패널을 횡력저항요소로 사용한 모듈러건물유닛 실험체 SDS와 SSP 모두 우수한 횡력저항성능에도 불구하고 주기거동 동안 핀칭이 크게 발생하여 에너지소산능력이 현저히 작았다.

5. 실험결과 분석 및 토의

실제 재료항복강도(Table 1 참조)를 사용하여 계산한 실험체의 강도 , 보정강도 , 항복변위 , 탄성강성 등을 계산하여 Table 2에 나타냈다. SDS 및 SSP 실험체는 원칙적으로 테두리골조가 횡력저항에 기여하지 못하므로, 내진설계를 위한 공칭설계강도 은 2장에 정리된 바와 같이 테두리골조의 영향을 무시하고 오직 스터드패널의 횡력저항만을 고려하여 식 (1)과 (8)로부터 계산하였다. 공칭항복변위 은 식 (2) 및 (9)를 사용하여 계산하였다. SDS와 SSP 실험체의 탄성강성 은 공칭강도 를 항복변위 로 나누어 구하였다.

은 테두리골조에 의한 횡력저항을 고려하여 계산한 SDS 및 SSP 실험체의 보정 강도를 나타낸다. 계산식은 Table 2의 주석에 나타냈다. 비록 SDS 및 SSP 실험체는 원칙적으로 테두리골조가 횡력저항에 기여하지 않지만, 3장 및 4장에서 설명한 바와 같이 실제 테두리골조의 보-기둥 접합부는 용접접합으로 제작하였고 다이어프램 강판으로 접합부를 보강한 결과 탄성영역에서 어느정도 횡력에 저항하였다. 따라서 보정강도 는 스터드패널과 테두리골조의 횡력저항을 합하여 계산하였다. 테두리골조는 기둥단면의 휨저항성능이 보에 비하여 작으므로, 보-기둥 접합면의 기둥 위험단면에서 휨항복이 발생한다고 가정하여 을 계산할 수 있다(Table 2 주석 참조). 다만, 4장과 Fig. 9 및 10의 파괴양상에서 설명한 바와 같이, 기둥 다이아프램의 용접부 파단이 초기탄성재하 동안에 발생하였으므로, 기둥 위험단면의 소성모멘트 대신 항복모멘트 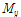(= , 여기서 = 기둥 강재의 항복강도, = 기둥의 탄성단면계수)를 사용하여 보정강도 를 계산하였다.

Table 2는 제안식과 실험으로 구한 강도, 항복변위, 탄성강성을 비교하여 보여준다. 예측된 강도, 항복변위, 탄성강성은 Fig. 8의 하중-변위 관계에도 나타냈다. 제안된 방법을 사용하여 이선형곡선으로 단순화된 하중-변위 관계는 점선으로 나타냈고( 및 ), 테두리골조의 영향을 고려한 보정강도 는 일점쇄선으로 나타냈다. 스트랩스터드패널을 이용한 SDS 실험체의 경우 실험 최대강도 가 공칭설계강도 보다 27∼29% 컸다. 그 이유는 첫째, 소성인장변형률을 보인 스트랩브레이스에 변형경화거동이 발생하였고, 둘째 테두리골조가 실험체의 횡력저항에 기여하였기 때문이다. 그러나 Fig. 9에 나타난 바와 같이 보-기둥 접합부에서 기둥 다이아프램 용접부 파단이 조기에 발생되므로, SDS 실험체의 최대강도 는 테두리골조의 횡력저항을 고려한 보정강도 보다 작았다. 시트강판스터드패널을 사용한 SSP실험체의 경우 실험 최대강도 가 공칭설계강도 보다 72% 컸고, 테두리골조의 영향을 포함한 보정 강도 보다도 크게 평가되었다. 이는 2장에 제안된 등가스트랩브레이스 모델에 의한 SSP 실험체의 공칭강도가 강판스터드패널의 횡력저항성능을 보수적으로 평가하였기 때문이다.

SDS의 항복변위 는 실제 항복변위 대비 작았고, 그 결과 탄성강성 이 실험값 대비 1.96 및 2.22배로 크게 평가되었다. 이는 스트랩을 스터드패널에 설치하는 과정에서 스트랩이 팽팽하지 않아 초기탄성재하 동안 강성이 감소된 것으로 판단된다. 따라서 안전한 내진설계를 위해서는 스트랩스터드패널의 횡강성을 약 50%로 줄여 구조설계를 수행하는 것이 바람직하다. 반면 시트강판스터드패널을 사용한 SSP는 실험에 의한 탄성강성 이 공칭탄성강성 보다 39% 및 40% 크게 평가되었다(Table 2 참조). 하지만, 보수적인 내진설계를 위해서는 강판스터드패널의 탄성 횡강성은 등가스트랩모델에 의한 탄성강성을 그대로 사용하는 것이 바람직하다.

6. 결  론

본 연구에서는 중력하중 및 횡하중에 저항하는 스터드패널을 이용한 모듈러건물유닛의 내진설계 방법을 제안하고, 실험을 통하여 모듈러건물유닛의 강성, 하중재하능력, 연성능력, 에너지소산능력 등 내진성능을 평가하였다. 모듈러건물유닛의 횡력저항요소로서 스트랩브레이스 및 시트강판으로 보강된 스터드패널을 적용하였다. 소성메커니즘을 근거로 모듈러건물의 내진설계를 위한 강도, 항복변위, 탄성강성 등 설계식을 제안하였고, 실험결과와 비교를 통하여 제안된 설계식을 검증하였다. 본 연구의 주요한 결과는 다음과 같다.

(1)스트랩브레이스 및 시트강판으로 보강된 스터드패널을 사용한 모듈러건물유닛은 초기탄성재하 동안 슬립변형이 없었고, 주기거동에서도 강성 및 강도저하가 크지 않은 안정적인 항복이후 연성거동을 보였다. 최대변위비 = 5.37%∼5.90%, 변위연성도 =5.76∼7.60의 우수한 변형능력을 보였다.

(2)스트랩스터드패널은 스트랩브레이스 인장항복에 의한 소성메커니즘에 의하여 지배되는 연성거동을 보였다. 스트랩브레이스, 거셋플레이트, 연결강판, 테두리보로 이어지는 하중전달 메커니즘은 스크류볼트 및 용접부의 파괴 없이 안정적으로 횡하중에 전달하였다. 다만, 박판의 스트랩을 팽팽하게 스터드패널에 붙이기 어렵고, 그 결과 실험으로 구한 실제 항복강성은 공칭값의 약 50%에 불과하였다. 따라서 구조설계 시 보수적으로 스트랩스터드패널의 횡강성을 50%로 줄이는 것이 바람직하다.

(3)시트강판스터드패널의 경우 모서리에만 스크류볼트를 배열하여 스터드패널의 횡력저항능력을 제어하였다. 실험결과 시트강판을 사용한 모듈러건물유닛 실험체는 우수한 강도, 변형능력 등 우수한 내진성능을 보였다. 다만, 시트강판을 스터드패널에 클래딩하기 위한 비구조용 스크류볼트가 횡력저항성능에 좋지 않은 영향을 미칠 수 있으므로 시트강판스터드패널 시공 상세에 주의하여야 한다.

(4)본 연구에서는 스트랩브레이스(스트랩브레이스를 사용한 모듈러건물유닛)와 등가스트랩브레이스(시트강판을 사용한 모듈러건물유닛)의 인장항복을 가정한 소성메커니즘을 바탕으로, 스터드패널을 사용한 모듈러건물유닛의 강도와 항복변위 평가방법을 개발하였다. 스트랩스터드패널의 강성을 제외하고, 제안된 설계식은 실제 스터드패널을 사용한 모듈러건물유닛의 강도, 강성, 항복변위 등 횡력저항성능을 합리적이면서 안전측으로 예측하였다.

스터드패널에 중력하중이 작용하는 경우 스터드의 압축력이 증가하여 모듈러시스템의 거동이 달라질 수 있다. 따라서 스터드패널을 이용한 모듈러건물유닛을 실제 건물에 적용하기 위해서는 중력하중을 받는 스터드패널 모듈러건물유닛의 횡력저항에 대한 후속 실험연구가 필요하다.

Acknowledgments

이 연구는 포스코와 정부(교육과학기술부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업(No. 2012 R1A1A1003282)의 연구비 지원을 받아 수행되었음.

References

•  이상섭, 배규웅, 박금성, 홍성엽(2013) 유닛 모듈러 기둥 - 보 조인트의 구조 성능에 대한 실험적 평가, 한국강구조회논문집, 한국강구조학회, 제25권, 제3호, pp.255-265.Lee, S.S., Bae, G.W., Park, K.S., and Hong, S.Y. (2013) An Experiment Evaluation of Structural Performance for the Beam to Column Joints in Unit Modular System, Journal of Korean Society of Steel Construction, KSSC, Vol. 25, No. 3, pp.255-265 (in Korean). [https://doi.org/10.7781/kjoss.2013.25.3.255]
• Hong, S.G., Cho, B.H., Chung, K.S., and Moon, J.H. (2011) Behavior of Framed Modular Building System with Double Skin Steel Panels, Journal of Constructional Steel Research, Vol. 67, No. 6, pp.936-946. [https://doi.org/10.1016/j.jcsr.2011.02.002]
• Annan, C.D., Youssef, M.A., and El Naggar, M.H. (2009) Experimental Evaluation of the Seismic Performance of Modular Steel-braced Frames, Engineering Structures, Vol. 31, No. 7, pp.1435-1446. [https://doi.org/10.1016/j.engstruct.2009.02.024]
• Moghimi, H. and Ronagh, H.R. (2009) Better Connection Details for Strap-braced CFS Stud Walls in Seismic Regions, Thin-walled Structure, Vol. 47, No. 2, pp.122-135. [https://doi.org/10.1016/j.tws.2008.07.003]
• Moghimi, H. and Ronagh, H.R. (2009) Performance of Light-gauge Cold-formed Steel Strap-braced Stud Walls Subjected to Cyclic Loading, Engineering Structures, Vol. 31, No. 1, pp.69-83. [https://doi.org/10.1016/j.engstruct.2008.07.016]
• Kim, T.W., Wilcoski, J., Foutch, D.A., and Lee M.S. (2006) Shaketable Tests of Cold-formed Steel Shear Panel, Engineering Structures, Vol. 28, No. 10, pp.1462-1470. [https://doi.org/10.1016/j.engstruct.2006.01.014]
• Adham, S.A., Avanessian, V., Hart, G.C., Anderson, R.W., Elmlinger, J., and Gregory, J. (1990) Shear Wall Resistance of Lightgauge Steel Stud Wall System, Earthquake Spectra, Vol. 6, No. 1, pp.1-14. [https://doi.org/10.1193/1.1585555]
• Fulop, L.A. and Dubina, D. (2004) Performance of Wall-stud Cold-formed Shear Panels Under Monotonic and Cyclic Loading, PartI: Experimental research, Thin-walled Structure, Vol. 42, No. 2, pp.321-338. [https://doi.org/10.1016/S0263-8231(03)00063-6]
• Al-Kharat, M. and Rogers, C.A. (2007) Inelastic Performance of Cold-formed Steel Strap Braced Walls, Journal of Construction Steel Research, Vol. 63, No. 4, pp.460-474. [https://doi.org/10.1016/j.jcsr.2006.06.040]
• 권영봉, 서응규, 임덕만, 김갑득, 권인규(2012) 복부에 슬릿이 있는 박판냉간성형형강 스터드의 압축강도, 한국강구조회논문집, 한국강구조학회, 제24권, 제2호, pp. 189-197.Kwon, Y.B., Seo, E.K., Lim, D.M., Kim, G.D., and Kwon, I.K. (2012) The Compressive Strength of Thin-Walled Cold-Formed Steel Studs with Slits in the Web, Journal of Korean Society of Steel Construction, KSSC, Vol. 24, No. 2, pp. 189-197 (in Korean). [https://doi.org/10.7781/kjoss.2012.24.2.189]
• Eurocode 3 (2004) Design of steel structures. Part 1-3: general rules. supplementary rules for cold-formed members and sheeting, CEN European Committee for Standardisation.
• Cassafont, M., Arnedo, A., Roure, F., and Rodriquez-Ferran, A. (2007) Experimental Testing of Joints for Seismic Design of Lightweight Structures. Part 3: Gussets, Corner Joints, X-braced Frame, Thin-walled Structures, Vol. 45, No. 7-8, pp.637-659. [https://doi.org/10.1016/j.tws.2007.05.008]
• 서건호, 서상정, 권영봉(2011) 국부좌굴이 발생하는 H-형강 휨부재의 강도에 관한 연구, 한국강구조회논문집, 한국강구조학회, 제23권, 제6호, pp.647-657.Seo, G.H., Seo, S.J., and Kwon, Y.B. (2011) A Study on the Moment Capacity of H-Section Flexural Members with Local Buckling, Journal of Korean Society of Steel Construction, KSSC, Vol. 23, No. 6, pp.647-657 (in Korean).