고력볼트로 체결된 T-stub의 지레작용력 및 부재 접촉력 예측모델

1. 서  론

인장력을 받는 접합부는 지레작용력과 부재 사이의 접촉력 등의 영향을 받아 예측한 설계강도보다 더 작은 강도에도 접합부가 파괴될 가능성이 있다. 그러므로 이러한 지레작용력과 부재 사이의 접촉력 등을 예측하기 위한 많은 연구들이 진행되었고, 이를 바탕으로 다양한 예측모델들이 제안되었다.

Douty와 McGuire[1]는 탄성해석에 근거하여 지레작용력을 예측하였다. 예측모델의 제안에 있어서 고력볼트와 연결부재의 재료적물성값 및 접합부의 기하학적 형상 등도 고려하였다. Agerskov[2]는 Douty와 McGuire와 같이 탄성해석에 근거하여 지레작용력을 예측하였다. Agerskov 예측모델은 고력볼트와 연결된 T-stub 플랜지의 변형, 전단변형의 영향 등도 고려하였다. 그러나 플랜지 항복에 따른 비선형성은 포함하지 않았다. Struik와 Back[3]은 고력볼트와 T-stub 플랜지 조합에 의한 일반적인 기하학적 형상을 갖는 접합부의 지레작용력을 예측하였다. 그러나 가장 널리 사용되는 Struik와 Back 예측모델은 실제 실험을 통하여 얻은 지레작용력보다 큰 값을 제공한다. Swanson[4],[5]은 부재 사이의 접촉력의 영향을 받아 고력볼트 축력의 중심선이 이동하는 것으로 가정하여 Struik와 Back의 예측모델을 개선한 예측모델을 제안하고 있으나 예측모델의 적용은 다소 복잡하여 졌다. Jaspart[6]와 Maquoi[7]는 고력볼트 초기장력에 따라서 발생하는 접합부 부재 사이의 접촉력 변화를 고찰하였고, 이러한 부재 사이의 접촉력 변화는 인장력을 받는 접합부의 인장강성에 영향을 준다는 것을 밝혔다. Faella 등[8],[9]은 접합부 부재 사이의 접촉력 변화를 연결 부재 플랜지의 휨강성과 고력볼트 축방향 강성 비 변화에 따라 고찰하였고, 이에 따른 접합부의 축방향 인장강성 변화를 예측하였다.

양재근 외[10]는 축방향 인장력을 받는 T-stub에 대한 거동파악을 위한 연구를 진행하였고, 이 연구는 그동안 제안된 지레작용력과 부재 사이의 접촉력 예측모델을 개선하기 위하여 진행되었다[11]. 이를 위하여 3차원 비선형 유한요소해석을 수행하였다[12]. 제안한 예측모델 적용의 타당성은 타 연구자의 해석결과와 비교·검토를 통하여 입증하였다.

2.상·하부 스플릿 T 접합부 3차원 비선형 유한요소해석

2.1 3차원 비선형 유한요소 해석을 위한 접합부 모델링

고력볼트로 체결된 접합부의 지레작용력과 부재 사이의 접촉력은 3차원 비선형 유한요소해석을 수행하여 예측하였다. 일반적으로 지레작용과 부재 사이의 접촉 효과는 접합부의 연결 플랜지가 상대적으로 얇고 고력볼트 게이지 거리가 큰 경우에 영향이 크다. Thornton[13]과 Astaneh[14]는 Kulak,의 연구결과를 바탕으로 지레작용효과의 영향을 파악하기 위하여 매개변수 을 아래의 식 (1)과 같이 제안하였다. 식 (1)의 제안에 있어서 는 지레작용효과를 받는 요소에 대한 고력볼트 구멍의 영향을 나타내는 변수로 플랜지의 순단면적과 총단면적의 비이며, 는 고력볼트 축력의 중심선에서 지레작용력 작용선과 고력볼트 축력의 중심선에서 T-stub 스템 표면까지의 거리 비로 정의할 수 있다. 의 값에 따라 T-stub의 파괴양상은 Fig. 1과 같이 3가지 타입으로 나눠지고 지레작용효과는 접합부의 기하학적 형상, 고력볼트 체결력, 접합부의 재료적 물성값의 영향을 받는 값이 1.0보다 큰 경우에 발생할 가능성이 높다. 그러므로 이 연구에서 고려한 접합부의 기하학적 형상은 Fig. 2와 Table 1에 정리한 것과 같이 값이 1.0보다 큰 접합부를 선택하였다.

 (1)

여기서,

(2)

(3)

(4)

(5)

(6)

접합부에 사용한 강재는 SS400 강종이며 재료적 물성값은 Fig. 3에 나타난 것과 같이 이중곡선모델(bilinear model)로 회귀분석 하여 Table 2와 같이 정리하였다. F10T-M20 고력볼트는 165kN의 초기장력을 주어 체결된 것으로 이상화 하였다.

고력볼트로 체결된 접합부는 상용프로그램인 ABAQUS (ver.6.9.2)[15]를 이용하여 모델링하였다. 접합부를 구성하는 T-stub은 C3D8R(eight-node brick element with reduced integration) 부재요소로, 고력볼트, 너트, 와셔 등은 C3D8 (eight-node brick element) 부재요소로 선택하여 모델링 하였다. 3차원 비선형 유한요소해석 시에 각 부재 사이에 발생하는 접촉과 지압, 고력볼트의 초기장력 등의 영향도 포함하여 모델링 하였다. 각 부재 사이의 미끄럼계수는 0.3으로 선택하였다. 전체 접합부 해석모델은 Fig. 4와 같이 총 11,738개의 부재와 총 19,000개의 절점으로 구성되었고, 한 모델의 해석수행은 약 30분이 소요되었다. 고력볼트로 체결된 접합부 모델링 시에 적용한 ABAQUS 옵션은 Table 3에 정리하였다.

2.2 3차원 비선형 유한요소 해석 결과

고력볼트로 체결된 인 T-stub가 축방향 인장력을 받으면 일반적으로 플랜지의 휨항복 후 소성변형에 의하여 접합부가 파괴된다. Fig. 5와 Fig. 6은 작용하중이 참조하중에 이르렀을 때의 접합부에 발생하는 응력분포를 나타내고 있다. 참조하중은 Richard 등[16]이 정의한 것과 같이 접합부 변형경화현상을 나타내는 구간의 기울기가 하중 축인 y-축과 만나는 절편 값을 의미한다. Fig. 5와 Fig. 6에 나타난 것과 같이 T-stub 필릿에서 일정한 거리 떨어진 부분 및 고력볼트 머리 내측 끝 단부와 T-stub 플랜지가 만나는 부분에 응력집중 현상에 의하여 휨항복이 발생하였다. 이러한 응력분포는 Faella et al. 및 Ballio와 Mazzolani[17]가 예측한 것과 같은 보 형태(beam pattern)의 소성힌지선을 나타내며 최종적으로 파괴한다.

3차원 비선형 유한요소해석결과 얻은 T-stub의 고력볼트 당 작용하중 - 고력볼트 축력 관계 곡선은 Fig. 7과 같다. 고력볼트 초기장력 165kN이 적용된 것을 확인할 수 있고, Struik와 Back이 T-stub 접합부 실험결과 얻은 고력볼트 당 작용하중 - 고력볼트 축력 관계 곡선과 매우 유사한 거동 양상을 나타낸다. 즉, 작용하중이 증가하면 고력볼트 축력도 점증적으로 증가하다가 참조하중을 지나면서 고력볼트 축력의 증가가 심화되어 최종적으로 고력볼트가 파단된다. 이러한 고력볼트 축력의 급격한 증가는 지레작용효과에 의한 것으로 판단한다. 즉, 매개변수 값이 큰 T-stub은 지레작용효과의 영향을 더 크게 받아 Fig. 7(a)에 나타난것과 같이 고력볼트 당 작용하중과 고력볼트 축력의 비도 100% 이상의 값을 나타낸다. 그러나 매개변수 값이 감소함에 따라서 지레작용효과의 영향도 함께 감소한다. 그러므로 매개변수 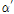값이 작은 T-stub은 Fig. 7(b)에 나타난 것과 같이 고력볼트 당 작용하중과 고력볼트 축력의 비도 100% 이하의 값을 제공한다. 또한, 지레작용효과가 없을 경우 Fig. 8과 같이 하중이 작용하면서 작용하중과 고력볼트 축력의 비율은 1:1로 나타나게 된다. Q/T 값은 지레작용효과에 의한 증가율로, 3차원 비선형 유한요소해석결과에 근거하면 고력볼트 축력의 평균증가율은 Table 4, Table 5, Table 6에 정리한 것과 같이 151%(3.67＜ ＜8.14), 66%(1.21＜ ＜1.95), 14% (0.07＜ ＜0.98)로 나타났다. Q/T 값은 의 영향을 받고 값이 클수록 Q/T 값은 크게 나타났다. 이 1.0보다 큰 기하학적 형상을 갖는 T-stub이 이 0＜ ＜1.0인 기하학적 형상을 갖는 T-stub보다 더 큰 지레작용 효과를 나타낸다.

2.3 고력볼트 초기장력에 의한 접촉력 분포양상

165kN의 초기장력으로 체결된 고력볼트에 의하여 고력볼트 머리, 와셔, T-stub 플랜지 사이에 발생하는 응력분포는 Fig. 9와 같은 양상을 나타낸다. 각 부재 사이의 접촉력 및 접합부의 플랜지와 고력볼트의 강성비는 이러한 응력분포에 의하여 영향을 받는다. 고력볼트 머리와 접합부 플랜지 사이에 접촉력은 와셔 끝부분을 시작으로 평균 9°(3.67＜ ＜ 8.14), 3°(1.21＜ ＜1.95), 1°(0.07＜ ＜0.98) 방향으로 영향을 미치는 것을 알 수 있다. Table 7, Table 8, Table 9에 정리한 것과 같이 유한요소해석결과 얻은 응력분포 사이각은 Faella et al.이 제안한 응력분포 사이각보다 작은 각도로 접촉력이 전달됨을 알 수 있다.

3. 지레 작용력 및 부재사이의 접촉력 예측모델

3.1 지레 작용력 예측모델

Struik과 Back는 Fig. 10과 같이 고력볼트로 체결된 접합부가 축방향 인장력을 받는 경우, 아래의 식 (7)과 같이 지레작용력, 과 작용축방향인장력, 의 비, 를 제안하였다. 식 (7)의 적용에 있어서 지레작용력은 플랜지의 끝 단부에 작용하는 것으로 이상화하였다.

 (7)

3차원 유한요소해석결과에 근거하여 과도한 (Q/T)를 제공하는 식 (7)에 수정변수 R을 적용하여 개선된 식 (8)을 아래와 같이 제안하였다. 수정변수 R은 유한요소해석결과 값과 비교하여 값에 따라 0.75( ), 0.77( ), 0.45( )으로 나타났고, 이를 파괴모드에 따라 Type Ⅰ일 경우 0.75, Type Ⅱ일 경우 0.45로 제안하였다. 식 (8)의 적용에 있어서 , 은 각각 고력볼트 축력의 중심선으로부터 플랜지의 끝 단부까지의 거리 및 고력볼트 축력의 중심선으로부터 스템까지의 거리로 정의 된다. 3차원 비선형 유한요소해석결과 얻은 응력분포에 의하면 고력볼트 축력의 중심선은 Fig. 11에 나타난 것과 같이 고력볼트 축의 중심선으로부터 만큼 이동한 것으로 이상화 할 수 있다.

 (8)

여기서,

 (9)

 (10)

 (11)

 (12)

3.2 고력볼트 축방향 인장강성 예측모델

Kulak 등[18]은 인장력을 받는 접합부의 고력볼트 축방향 인장강성을 아래의 식 (13)과 같이 제안하였다. 식 (13)의 계수 1.6은 지레작용력의 영향을 포함한 계수로 Fig. 12과 같이 T-stub에 축방향 인장력 T가 작용할 때 볼트 축력 B를 0.63T로 가정하여 고력볼트 축방향 인장강성을 나타낸 것이다. 지레작용력이 작용하지 않는 Type Ⅲ의 파괴형태인 경우는 볼트 축력 T가 0.5T가 되어 지레작용효과 계수는 2.0이 된다.

 (13)

여기서,

 (14)

식 (8)의 Yang 해석모델을 고력볼트 축방향 인장강성에 적용하여 식 (15)와 같이 나타내었고, 이를 14개의 해석모델에 대해 T-stub 두께와 고력볼트 게이지 거리를 변수로 식 (13)의 1.6과 같이 지레작용효과 계수의 관계를 Fig. 13, Fig. 14와 같이 나타내었다. 지레작용효과 계수는 T- stub 두께와 비례, 고력볼트 게이지 거리와는 반비례함을 알 수 있었고, 이를 통해 Fig. 15와 같이 값과 선형적인 관계를 확인하였다. 고력볼트 축방향 인장강성은 T-stub 플랜지 두께가 두꺼워지고 고력볼트 게이지 거리가 짧을수록 증가하고 지레작용력 Q/T와 고력볼트 축방향 인장강성은 반비례함을 알 수 있다. 즉, Type II의 거동양상을 나타내는 T-stub 접합부 해석모델은 Kulak 등[18]이 제안한 1.6의 계수와 매우 유사한 지레작용력 계수 값을 제공한다. 또한, 고력볼트의 축방향 인장강성을 Fig. 15와 같은 비로 정리하면 다음의 식 (16)과 같이 정리할 수 있다.

 (15)

 (16)

3.3 부재 사이의 접촉력 예측모델

Faella et al.은 Fig. 16과 같이 고력볼트의 초기장력에 의한 고력볼트 머리와 접합부 플랜지 사이에 접촉력이 45° 방향으로 영향을 미치는 것으로 가정하였다. 또한, Faella et al.은 이러한 접촉력의 영향을 받는 접합부의 플랜지와 고력볼트의 강성비, 를 아래의 식 (17)과 같이 제안하였다. 여기서, , , 등의 값이 일반적으로 적용된다. Faella et al.에 의하여 제안된 식 (17)은 Agerskov[2] 및 Bursi[19]가 제안한 에 관한 식들을 적용한 값과도 유사한 값을 제공한다.

 (17)

이 연구에서는 3차원 유한요소해석을 통한 응력분포 사이각에 근거하여 최대 평균사이각 9˚를 선택하고 접합부의 플랜지와 고력볼트의 강성비를 아래의 식 (18)과 같이 제안했다. 식 (18)은 Faella et al.이 제안한 식 (17)의 값보다 더 작은 값을 제공한다.

 (18)

3.4 고력볼트로 체결된 T-stub의 지레작용력 산정

제안한 지레작용효과 예측모델 식 (8) 적용의 타당성은 Hantouche[20]가 수행한 Fig. 17의 T-stub 해석결과와 비교․검토하여 검증하였다. Fig. 17에 나타난 Hantouche의 T-stub 유한요소 해석모델을 동일한 기하학적 형상, 재료적 물성값, 경계조건, 하중조건 등을 적용하여 3차원 비선형 유한요소 해석을 재수행하였다. 재수행한 유한요소해석결과 얻은 T-stub 모델의 응력분포는 Fig. 18과 같다. Fig. 19에 나타난 것과 같이 Yang의 T-stub 재해석결과 얻은 고력볼트의 지레작용효과는 Hantouche의 T-stub 해석결과 얻은 고력볼트의 지레작용효과와 매우 유사한 지레작용효과를 제공하고 있다. Hantouche 해석모델은 식 (19)와 같고 Table 10, Table 11과 같이 Yang 해석모델과 큰 차이를 보이지 않는다. 그러나 Hantouche 해석모델은 식 (21)과 같이 유한요소해석을 통한 계수 를 포함하고 있다. 따라서 Yang 해석모델을 적용하는 것이 좀 더 쉽게 Q/T 값을 얻을 수 있다.

 (19)

여기서,

 (20)

 (21)

 (22)

4. 결  론

본 논문에서는 인장력을 받는 고력볼트로 체결된 T-stub 접합부의 지레작용력과 부재 사이의 접촉력을 예측할 수 있는 개선된 해석모델을 제공하기 위하여 진행하였다. T-stub 플랜지 두께와 고력볼트 게이지 거리를 변수로 선정하여 총 14개 모델에 대한 유한요소해석을 수행하였다. 이 연구를 통하여 다음과 같은 결론을 얻었다.

(1)3차원 비선형 유한요소해석결과에 근거하면 고력볼트 당 작용하중-고력볼트 축력관계 그래프에서 Q/T 값은 1.51 ( ), 0.66( ), 0.14 ( )으로 의 영향을 받고 값이 클수록 Q/T 값은 크게 나타났다. 따라서 Type I의 기하학적 형상을 갖는 T-stub이 Type II의 기하학적 형상을 갖는 T-stub보다 더 큰 지레작용효과를 나타냈다.

(2)고력볼트 축방향 인장강성은 T-stub 플랜지 두께가 두꺼워지고 고력볼트 게이지 거리가 짧을수록 증가하고 지레작용력 Q/T 값과 반비례한다. Kulak et al.이 제안한 1.6의 지레작용효과 계수는 시험체 중 G140-T28- B230(1.64)와 유사한 값을 나타내었다.

(3)3차원 비선형 유한요소해석결과 얻은 고력볼트 머리와 접합부 플랜지 사이의 접촉력은 응력분포 사이각의 영향을 받으며 Faella et al.이 제안한 값보다 작게 나타났다.

(4)T-stub 접합부의 Q/T 예측에 있어서 Yang 해석모델은 Table 10 및 Table 11에 나타난 것과 같이 Hantouche 해석모델과 유사한 값을 제공하였다. 그러나 Hantouche 해석모델은 복잡한 유한요소해석이 반드시 필요하므로, Yang 해석모델을 적용하는 것이 좀 더 쉽게 Q/T 값을 예측할 수 있다.

기 호

 :고력볼트의 공칭단면적( )

 :고력볼트 초기장력

 :강재의 탄성계수( )

 :강재의 할선계수( )

 :강재의 항복강도( )

 :강재의 인장강도( )

 :T-stub의 지레작용력

 :T-stub의 참조하중

 :고력볼트 중심축과 T-stub 플랜지 끝 단 사이의 거리( )

 :고력볼트 중심축과 T-stub 스템 면 사이의 거리( )

 :T-stub 플랜지 폭( )

 :고력볼트의 직경( )

 :고력볼트 구멍의 직경( )

 :T-stub의 고력볼트 게이지 거리( )

 :고력볼트의 축인장강성( )

 :고력볼트의 피치( )

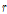 :필릿 반경( )

 :T-stub 플랜지의 두께( )

:T-stub 플랜지와 접하는 플랜지의 두께( )

 :고력볼트헤드의 두께( )

 :너트의 두께( )

 :T-stub 웨브의 두께( )

 :와셔의 두께( )

 :1.0 (A325 bolts), 0.88 (A490 bolts)

 :특정 두께에 대한 고력볼트가 받는 인장 강도를 극대화 하거나 주어진 고력볼트가 받는 인장 강도에 필요한 두께를 최소화 하는 값

 :강재의 인장 변형률

Acknowledgments

이 논문은 한국연구재단(과제번호 2012-047786)과 인하대학교의 지원에 따른 연구결과를 종합한 것이다. 이에 저자들은 감사의 뜻을 표합니다.

References

• Douty, R.T. and McGuire, W. (1965) High strength bolted moment connections, J. Struct. Div., ASCE, Vol. 91, No. 2, pp.101-128.
• Agerskov, H. (1976) High strength bolted connections subject to prying. Journal of Structural Engineering Div., ASCE, Vol. 102, No. 1, pp.161-175.
•  Struik, J.H.A. and de Back, J. (1969) Tests on bolted T-stubs with respect to bolted beam-to- column connections, Report 6-69-13, Stevin Laboratory, Delft University of Technology, Delft, The Netherlands.
• Swanson, J.A. (1999) Characterization of the strength, stiffness, and ductility behavior of T-stub connections, Ph.D. Dissertation, Georgia Institute of Technology, Atlanta, USA.
• Swanson, J.A. (2002) Ultimate strength prying models for bolted T-stub connections, Engineering Journal, AISC, Vol. 39, No. 3, pp.136-147.
• Jaspart, J.P., Steenhuis, M., and Weinand, K. (1995) The stiffness model of Revised Annex J of Eurocode 3, Proceedings of 3rd International Workshop on Connection in Steel Structures, Trento, pp.28-31.
• Jaspart, J.P. and Maquoi, R. (1995) Effect of bolt preloading on joint behaviour, Steel Structures, Eurosteel ’95, edited by Kounadis, Balkema.
• Faella, C., Piluso, V., and Rizzano, G. (1996) Some proposals to improve EC3-Annex J Approach for predicting the moment-rotation curve of extended end plate connections, Costruzioni Metalliche, No. 4.
• Faella, C., Piluso, V., and Rizzano, G. (1998) Experimental analysis of bolted connections: snug versus preloaded bolts, Journal of Structural Engineering, ASCE, Vol. 124, No. 7,  pp.765-774. [https://doi.org/10.1061/(ASCE)0733-9445(1998)124:7(765)]
• Yang, J.G., Park, J.H., and Back, M.C. (2012) Prediction models for the prying action force and contact force of a T-stub fastened by high- strength bolts, Proceedings of Annual AIK Conference, AIK, pp.465-466.
• AISC (2010) Steel Construction Manual, 14th Ed., American Institute of Steel Construction, Chicago, II. pp. 9-10 - 9-13.
• Lemonis, M.E. and Gantes, C.J. (2006) Incremental modeling of T-stub connections, Jounal of Mechanics of Materials and Structures, Vol. 1, No. 7, pp. 1135-1159. [https://doi.org/10.2140/jomms.2006.1.1135]
• Thornton, W.A. (1985) Prying action: A general treatment, Engineering Journal, AISC, Vol. 22, No. 2, pp.67-75.
• Astaneh, A. (1985) Procedure for a design and analysis of hanger-type connections, Engineering Journal, AISC, Vol. 22, No. 2,  pp.63-66.
• ABAQUS. (2007) User's manual, I-IV(Version 6.9).
• Richard, R.M., Hsia, W.K., and Chmielowiec, M. (1988) Derived moment-rotation curves for double- framing angles, Comput & Struct, Elsevier Science Ltd., 3, pp.485-494. [https://doi.org/10.1016/0045-7949(88)90281-7]
• Ballio, G. and Mazzolani, F.M. (1994) Strutture in A cciaio. Hoepli, Milan.
• Kulak, G.L., Fisher, J.W., and Struik, J.H.A. (2001) Guide to design criteria for bolted and riveted joints, 2nd Ed., American Institute of Steel Construction, New York.
• Bursi, O. (1990) Behaviour of high strength bolts in bolted beam-to-column connections, Proceedings of Applied Stress Analysis Conference, Nottingham.
• Hantouche, E.G. (2011) Behavioral characterization of built-up T-stub connections for use in moment resisting frames, Ph.D. Dissertation, University of Cincinnati, Cincinnati, USA.