1. 서  론

강구조 건물의 일반적인 해석 및 설계에서 기둥-보 접합부의 이상적인 구조적 거동을 강(rigid)접합 또는 단순(simple)접합으로 취급하지만, 실제로는 철판, 앵글, 볼트 등과 같은 접합부 구성요소들의 순차적인 항복으로 인한 비선형 거동을 나타내는 반강(semirigid)접합으로 고려되어야 한다. 강구조 건물의 안정성 확보를 위해서는 반강접으로 분류되는 여러 가지 접합부의 강도 및 회전강성을 명확히 파악하여 실질적인 거동특성을 설계에 반영하여야 한다. 반강접 접합부의 한 형태인 더블 웨브앵글 접합은 사용하중 하에서 큰 마찰력이 요구되지 않는 지압볼트를 통하여 보에서 기둥으로 전단력이 전달되도록 설계되며, 주로 H형강 기둥과 보로 설계되는 중·저층 건물에 적용된다.

지금까지 H형강 기둥-보의 더블 웨브앵글 접합부가 갖는 강도와 강성을 파악하기 위하여, 보 웨브 강성에 의한 지압이 앵글의 거동에 미치는 영향과 앵글의 기하학적 형상, 볼트의 개수 및 크기에 따른 모멘트-회전각 관계 및 전단력-회전각 관계 등에 대한 다양한 실험과 해석연구가 수행되었다^{[1],[2], [3],[4],[5],[6],[7],[8]}.

 또한, Lother^[9]는 더블 웨브앵글 접합부의 탄성해석에 근거하여 접합부의 초기 회전강성관한 선형모델과 허용 저항 모멘트 능력을 예측식을 통해 제안하였고 Frye 등^[10]은 재료의 거동이 선형이고 접합부의 변형에 미치는 전단력과 축력의 영향을 무시한다는 가정을 전제로, Sommer^[6]에 의해 개발된 모델을 기본으로 하여 다항식 형태의 모델식을 제안하였다.

CFT(Concrete Filled Steel Tube)구조는 원형 혹은 각형단면의 강관내부에 콘크리트를 충전한 구조로 강관과 충전콘크리트의 상호 합성작용에 의하여 강성, 내력, 변형성능, 내화, 시공 등의 측면에서 우수한 특성을 발휘하는 구조시스템이다. 특히, 반복하중의 작용에 대해서는 우수한 내진성능을 발휘하고 경제성이 우수하며 범용성이 높아 사용이 증가하고 있는 추세이다. 하지만 우리나라에서는 콘크리트 충전성 확보 및 품질 검사 어려움, 내진성능을 갖춘 접합부 개발의 부족 및 규격화와 표준접합부상세 제공 부족 등으로 실무에 많이 적용되지 않는다. 일반적으로 CFT 기둥과 보의 접합부에는 접합부의 응력집중이나 변형에 대한 보강을 위하여 다이아프램을 사용하는데, 이러한 경우 용접에 대한 주의가 반드시 필요하게 되며, 또한 내측 또는 관통 다이아프램을 사용할 경우에는 콘크리트의 충전성에 주의해야 한다.

본 연구에서는 다이아프램의 이용을 배제하고 높은 연성 및 시공성을 확보하기 위하여, 강봉과 더블 웨브앵글을 이용한 CFT 기둥-보 접합부에 대한 상세를 제공하였다. 반복하중을 받는 CFT 기둥-보의 앵글 접합부의 거동 예측과 휨모멘트 내력을 파악하기 위한 국내의 연구는 아직 미흡하며, 설계에 필요한 접합부 상세 개발 및 설계지침 제안 등이 본격적으로 이루어지고 있지 않은 실정이다. 그러므로 본 연구에서는 앵글 두께 및 강봉의 게이지 거리를 변수로 선택하여 3차원 유한요소 해석을 통하여 반복하중을 받는 CFT 합성골조의 더블 웨브앵글 접합부의 모멘트-회전각 관계 변화를 파악하고 회전강성, 휨모멘트 내력, 응력분포 및 파괴모드를 분석하여 구조적 거동을 알아보고자 한다.

2. 3차원 유한요소 해석모델

더블 웨브앵글을 이용한 CFT 기둥과 H형강 보의 접합부에 대한 기하하적인 형상 및 크기가 Fig. 1에 나타나 있다. 이 때 CFT 기둥의 높이와 H형강 보의 길이는 각각 3,200 mm와 2,150 mm이며, 2개의 웨브앵글 및 8개의 강봉과 8개의 볼트로 연결되어 있다. Fig. 2에서와 같이 범용유한요소해석 소프트웨어인 ANSYS^[11]를 이용하여 접합부의 각 부재(즉, 각형강관, 콘크리트, H형강, 앵글, 강봉, 볼트)에 대한 3차원 유한요소모델링이 이루어졌다. 이러한 모델링 과정에서 강재의 재료 및 기하학적인 비선형을 지원하는 ANSYS의 3차원 요소인 Solid 185와 CFT 기둥의 콘크리트의 재료적 특성을 포함하는 3차원 요소인 Solid 65가 적용되었다. Fig. 2의 확대된 웨브앵글, 볼트, 강봉 및 CFT 기둥의 콘크리트의 유한요소모델로부터 응력집중이 발생될 가능성이 있는 부분에 더욱 세밀한 요소망이 형성되어있음을 볼 수 있다. CFT 기둥 양쪽 끝단의 경계조건은 고정으로 하였으며 하중은 H형강 보의 자유 단부에 가해지는 변위제어법을 이용하였다. 변위하중은 Fig. 3과 같이 AISC 내진설계 매뉴얼^[12]에서 제시한 단조증가 반복하중이력을 이용하였다.

 (1)

여기서, ( )는 주응력이며, 주응력의 위첨자 p는 소성응력을 나타낸다.

또한, 직경이 22 mm(M22)인 F10T 볼트 및 강봉을 체결할 때 축방향으로 발생되는 프리텐션을 고려해야 하는데, 본 연구의 유한요소 해석모델에서는 현행 기준(KBS2009)에 제시된 200kN의 프리텐션 값을 주었다. 더블 웨브앵글을 이용한 CFT 기둥-보 접합부는 각형강관, 콘크리트, 앵글, 볼트 등과 같이 다양한 부재와 재료들로 구성되어 있기 때문에, 이러한 부재들 사이의 상호작용은 매우 다양하게 고려되어야 한다. 일반적으로 이러한 상호작용은 부재들 사이의 접촉면 상태에 따라 달라지며, 엄밀한 3차원 비선형 유한요소해석을 수행할 경우, 실제 접촉면과 가까운 접촉조건을 적용해야한다.

Table 3에서와 같이 CFT 기둥-보 접합부에 사용되는 앵글의 길이, 볼트와 강봉의 수, 직경 및 피치거리는 일정하다고 가정하였다. 다른 한편으로, 앵글 두께 및 게이지 거리의 변화에 따른 더블 웨브앵글 접합부의 응력 및 변형 등과 같은 구조적 거동에 대한 경향을 파악하기 위하여, 앵글 두께 를 12 mm, 15 mm, 19 mm로 변화시켰으며, 강봉의 게이지거리 는 65 mm와 90 mm로 두 가지 경우를 고려하였다(Table 3 참조).

3. 정적해석

3.1 휨모멘트 내력

Fig. 5는 정적하중(보 자유단의 최대변위 = 130 mm)을 받는 CFT 기둥-보 접합부의 휨모멘트와 회전각의 관계를 앵글 두께 및 강봉의 게이지 거리의 변화에 따라 나타낸 것이다. 예측한바와 같이, 고려되고 있는 두 가지 게이지 거리(즉, 65 mm와 90 mm)에 대해서 앵글 두께가 증가하면 초기회전강성, 참조모멘트(항복모멘트) 및 휨모멘트 내력도 증가함을 알 수 있는 반면, 앵글 두께와 관계없이 게이지 거리가 커지게 되면 초기회전강성, 참조모멘트 및 휨모멘트 내력은 감소하게 된다(Fig. 5 참조). 이와 같은 각 유한요소해석모델의 휨모멘트-회전각 관계 곡선은 회기분석을 통한 이론적 접근방법과의 결과검증이 이루어질 필요가 있다.

Richard^[13],[14]가 제안한 식 (2)를 적용하면 정적하중을 받는 CFT 기둥-보 접합부의 거동양상을 예측하는데 필요한 변수인 초기회전강성, 소성회전강성, 참조모멘트 및 곡선형태변수 등을 얻을 수 있다.

(2)

여기서,    :초기회전강성

         :소성회전강성

         :모멘트

         :참조모멘트

         :곡선형태변수

         :회전각

Fig. 5의 각 유한요소해석모델의 휨모멘트-회전각 관계 곡선은 상용프로그램인 SigmaPlot(version 8.0)으로 식(2)의 Richard 해석모델을 적용하여 회귀분석 하였다. Fig. 6은 G90-T12에 대한 휨모멘트-회전각 관계 곡선의 전형적인 회기분석 결과를 나타내고 있다. Fig. 6에서 전이모멘트 구간을 통과하기 이전의 휨모멘트-회전각 관계 곡선의 기울기는 접합부의 초기회전강성 에 해당하며, 전이모멘트 구간을 지난 후의 곡선의 기울기는 접합부의 소성회전강성 에 해당한다. 또한, 참조모멘트 는 접합부의 모멘트경화현상을 나타내는 구간의 기울기가 모멘트 축과 만나는 값을 의미하며, 곡선형태변수 은 전이모멘트 구간의 실제 휨모멘트-회전각 관계 곡선과 회귀분석을 통하여 얻은 전이모멘트 구간의 적합성을 나타낸다.

본 연구에서 고려된 모든 경우에 대해서 동일한 방법의 회귀분석이 이루어졌으며, 이를 통하여 얻은 초기회전강성, 소성회전강성, 참조모멘트, 곡선형태변수 등의 값을 Table 4에 정리하였다. Table 4에 제시한 값들은 더블 웨브앵글 접합부의 탄성거동 및 소성거동을 파악하는데 매우 중요하다는 것을 주지해야 한다. 앵글 두께가 클수록, 강봉의 게이지 거리가 작을수록 초기회전강성 값의 증가는 뚜렷하게 나타난다. 일반적으로, 회귀분석 결과의 적합성은 결정계수(coefficient of determination) 값을 이용하며, 결정계수 값이 1.0에 접근할수록 실제의 휨모멘트-회전각 관계곡선과 적합하다고 판단된다. Table 4에서의 결정계수의 값들이 0.99이므로 본 연구에서 수행된 회귀분석 결과가 매우 적합하다는 것으로 판단될 수 있다.

3.2 소성휨모멘트 해석모델

일반적으로 더블 웨브앵글 접합부에 작용하는 하중이 더욱 증가하면 최종적으로 앵글 단변의 용접부가 파단하면서 접합부가 파괴된다. 따라서 작용하중으로 인하여 전단 및 휨모멘트를 동시에 받는 앵글의 항복에 대한 영향을 파악하고 이를 근거로 접합부의 소성휨모멘트를 산정하는 것은 매우 중요하다. 휨모멘트를 받는 더블 웨브앵글 접합부의 실험 및 3차원 비선형 유한요소해석을 통하여 양재근 등^[2]은 Chen 등^[15]이 제시한 소성휨모멘트 해석모델에 대해 소성힌지가 발생하는 위치를 수정하여 제안하였다.

Chen이 제안한 소성힌지항복선(plastic hinge line)은 Fig. 7과 같이 앵글 상부 끝단의 볼트머리 중심에서 필릿부에 생성된 것이 앵글의 하부에서 만나게 된다고 하였다. 앵글 끝단에서 만큼 떨어진 곳에서의 단위길이에 대한 소성휨모멘트 와 전단력 를 갖으며 이때의 일의 평형방정식은 식 (3)과 같고 이를 통하여 더블 웨브앵글 접합부의 소성휨모멘트를 구할 수 있다. 와 를 Druker 및 Tresca의 항복이론을 적용하면 식 (4)와 같이 정리되며 간단한 정역학을 이용하면 식 (5)와 같이 얻을 수 있다. 식 (5)의 적용에 있어서 앵글의 작용하는 단위길이 당 전단력인 는 비선형으로 변화하나 선형으로 변화하는 것으로 가정하고, 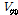는 앵글 상부( )에서 최소값 를, 앵글 하부( )에서 최대값 를 갖는 것으로 정하였다. 접합부의 극한모멘트 식은 (6)과 같다.

 (3)

 (4)

여기서,   

        : 단위길이에 대한 순수 전단력

        : 순수 소성휨모멘트

        : 단위길이에 대한 소성휨모멘트

 (5)

 (6)

그러나 보다 엄밀한 실험과 해석 결과를 통하여 응력이 집중되는 곳을 중심으로 생성되는 소성힌지항복선을 근거로 양재근 등^[2]은 Fig. 8과 같은 소성힌지항복선을 제안하였다. 볼트 외측에서 생성된 앵글 상부의 소성힌지항복선은 앵글 필릿부로 경사지게 폭이 줄어들다 최하부에서 앵글 필릿 끝부분에 생성된다. 즉, 앵글 하부에서 소성힌지 항복선이 만난다고 Chen 등^[15]이 가정한 것과는 다르게 앵글 하부에서 필릿 반경만큼 떨어진 부분에 생성된다. Fig. 8에서 제안한 소성힌지항복선을 이용하는 경우, 대신 를 적용하여 식 (7)에 대입한 후에 식 (6)을 이용하면 더블 웨브앵글 접합부의 소성휨모멘트를 구할 수 있다.

여기서, 

      : 고정단 앵글 장변과 기둥 플랜지간의 사이각

Table 5는 3차원 유한요소해석(FEA)을 통하여 얻은 소성휨모멘트 값과 앞에서 언급한 Chen 등(1988) 및 Yang 등(2006)이 제안한 이론적 접근방법(이하, 각각 Chen's model 및 Yang's model)을 적용하여 얻은 값들을 정리한 것이다. Table 5로부터 모든 앵글 두께와 게이지 거리에 대해 향상된 Yang 모델의 소성휨모멘트 값이 Chen 모델의 소성휨모멘트 값보다 항상 크게 산정되는 것을 알 수 있다.

Table 5는 게이지 거리가 65 mm인 경우 앵글 두께가 12 mm(즉, G65-T12)일 때 본 연구의 결과와 Yang 모델의 결과가 7.63%로 가장 근접하는 것으로 나타났으며, 앵글의 두께가 증가할 때 두 결과 사이의 차가 40.85%까지 커지는 경향을 보이고 있다. 반면, 게이지 거리가 90 mm인 경우 앵글 두께가 15 mm(즉, G90-T15)일 때 3.43%로 가장 근접하는 것으로 나타났으며 두께가 가장 큰 G90-T19에서 31.97%로 가장 큰 차이가 나타는 것을 볼 수 있다. Table 5의 유한요소해석 결과와의 비교로부터 소성휨모멘트를 이론적으로 구하기 위한 식(6)은 앵글 두께의 변화가 고려되지 않은 것으로 판단될 수 있으며, 향후 앵글 두께의 변화에 따른 소성휨모멘트 산정식이 새롭게 제안되어야 할 것이다.

4. 동적해석

앞 절에서 다루어진 정적하중에 대한 6가지의 CFT 기둥-보 접합부 해석모델(Table 3 참조)의 모멘트-회전각 이력곡선을 얻기 위하여 Fig. 3과 같은 단조증가 반복하중이력을 적용하였다. 반복하중을 받는 더블 웨브앵글 접합부의 파괴모드는 이력곡선의 거동과 과 응력분포의 형상으로부터 결정될 수 있으며, 일반적으로 다음과 같이 2가지 형태로 구분될 수 있다^[16].

(i) 볼트직경에 비하여 앵글 두께가 얇은 경우: 앵글의 과도한 소성화

(ii) 볼트직경에 비하여 앵글 두께가 두꺼운 경우: 볼트파괴

Fig. 9는 게이지 거리가 65 mm로 일정한 경우 앵글 두께가 12 mm와 19 mm인 더블 웨브앵글 접합부의 모멘트-회전각 이력곡선을 보여주고 있으며, Fig. 10과 Fig. 11에는 최대 변위하중 하에서 이에 상응하는 접합부의 각 부재(즉, H형강 보, 앵글, 강봉, 볼트)의 변형도와 von Mises 응력분포를 나타내었다. Fig. 9로부터 동일한 게이지 거리에서 앵글 두께가 큰 경우 초기강성이 더 큰 것으로 나타나는 것을 알 수 있으며(정적해석 결과와 동일함), 에너지 소산능력도 다소 다른 핀칭(pinching) 효과를 갖고 증가함을 알 수 있다. 여기서 핀칭은 반복하중 동안 발생되는 항복값을 갖는 재료에서의 영구변형의 결과를 말한다.

Fig. 10과 Fig. 11로부터 게이지 거리가 65 mm인 경우에 앵글 두께에 관계없이 접합부 부재의 최대 von Mises 응력은 강봉에서 발생함을 알 수 있었으며, 앞에서 언급한 파괴모드 (ii)에 해당하는 것으로 간주될 수 있다. 앵글 두께가 12 mm인 경우 최대 응력(737.8 MPa)이 앵글의 필릿부 끝단에서 발생했으며(Fig. 10(b) 참조), 앵글 두께가 19 mm인 경우 최대 응력(517.2 MPa)이 볼트구멍에서 발생하여(Fig. 11(b) 참조) 앵글 두께에 따라 앵글의 변형형상 및 응력분포가 달라진다는 것을 알 수 있다.

Fig. 12는 게이지 거리가 90 mm로 증가시킨 경우 두께를 12 mm와 19 mm로 한 더블 웨브앵글 접합부의 모멘트-회전각 이력곡선을

Fig.

Fig. 15는 최대 변위하중 하에서 이에 상응하는 G65-T19 접합부의 CFT 기둥내부의 콘크리트에 발생하는 전형적인 von Mises 응력분포를 보여주고 있으며, 최대응력은 본 해석에서 가정한 콘크리트의 최대압축응력인 약 27 MPa로 나타났다. 접합부 쪽의 응력분포를 나타내고 있는 Fig. 15(a)로부터 최대응력이 하부 볼트구멍 주위에 발생하고 있는 반면, 접합부 반대편의 응력분포를 나타내고 있는 Fig. 15(b)로부터 최대응력이 강봉 구멍 주위에 비교적 균등하게 분포되어 있는 것을 알 수 있다. Table 6에 동적하중에 대한 6가지의 CFT 기둥-보 접합부 해석모델에 대한 초기강성, 최대응력, 최대휨모멘트 및 최대회전각을 요약하였으며, 이러한 것들은 더블 웨브앵글의 반강접을 갖는 CFT 합성골조의 비선형 동적해석에 필요한 기초적 데이터베이스가 될 것이다.

본 연구에서는 반복하중을 받는 CFT 합성골조 더블 웨브앵글 접합부의 앵글 두께 및 강봉의 게이지 거리를 변수로 적용하여 3차원 비선형 유한요소해석을 수행하였다. 해석결과로부터 더블 웨브앵글 접합의 휨모멘트 내력, 초기회전강성, 소성회전강성, 소성휨모멘트, 응력분포 및 파괴모드를 분석하여 다음과 같은 결론을 얻었다.

(1)CFT 합성골조 기둥-보의 더블 웨브앵글 접합부는 앵글의 두께와 강봉의 게이지 거리의 변화에 따라 접합부의 각 부재의 응력분포가 달라지며, 이에 따른 파괴모드 및 변형형상이 달라진다. 앵글의 두께가 커질수록, 또 강봉의 게이지 거리가 작아질수록 초기강성 및 휨모멘트 내력이 증가한다.

(2)휨모멘트-회전각 이력곡선으로부터 앵글의 두께가 커질수록, 또 강봉의 게이지 거리가 작아질수록 에너지 소산 효과가 증가하는 것을 볼 수 있었다.

(3)접합부의 최대회전각 0.04 radian에 상응하는 CFT 기둥 내부 콘크리트의 최대압축응력은 약 27 MPa이며, 더블 웨브앵글의 하부 볼트구멍 주위에 응력이 집중되어 있는 것으로 나타났다.

향후, 더블 웨브앵글 접합부를 갖는 여러 가지 구조물의 거동을 알아보고 이해하기 위해서는 파라미터를 더욱 다양하게 적용시킨 해석적 연구와 이를 검증하기 위한 실험적 연구가 수행되어야 할 것이다.

기  호

   탄성계수

   강봉 중심에서 앵글 단변의 끝단까지의 거리

    게이지 거리

   초기회전강성

   소성회전강성

    앵글의 길이

   휨모멘트

   참조모멘트

   순수 소성휨모멘트( )

  단위길이에 대한 소성휨모멘트

    곡선형태변수

   단위길이에 대한 순수 전단력의 최대값

  단위길이에 대한 순수 전단력의 최소값

  단위길이에 대한 순수 전단력

    프아송비

    앵글의 두께

    회전각

   고정단 앵글 장변과 기둥 플랜지간의 사이각