수평적 공간변이 지진에 대한 고속열차-궤도-교량 시스템의 확률 해석
Copyright © 2019 by Korean Society of Steel Construction
초록
본 연구는 유사가진법(PEM)을 확장해서, 전파통과 효과나 비간섭 효과와 같은 지반 운동의 공간적 효과들이 조합되어 열차-궤도-교량 시스템(TTBS)의 지진응답에 미치는 영향을 조사한다. 열차는 현가장치들에 의해 연결된 강체들로, 궤도와 교량은 유한요소들로 모델을 구축한다. 차륜/궤도 강체 접촉을 고려하여, TTBS의 운동방정식을 유도한다. 간섭 모델에 기초하여 지반 가속도의 파워 스펙트럼(PSD) 행렬을 구성하고, 이 PSD 행렬을 분해하여 일련의 유사가진들을 구축한다. 이 유사가진들에 대한 TTBS의 유사응답 PSD를 사용하여 표준편차들을 산출한다. 수치 예제에서, 고속열차가 주행하는 20경간 단순교의 지진응답을 열차와 교량의 측면 가속도를 통해 평가한다. 해석 결과들은 지진의 비간섭 효과가 TTBS의 지진응답에 매우 중대한 영향을 미침을 보여 준다. 또한, 지진파의 겉보기 속도가 더 빠르고 최대 지진 가속도가 더 클수록 TTBS의 측면 가속도는 매우 증가한다.
Abstract
This study extended the pseudo-excitation method (PEM) to investigate the combined influence of spatial effects, such as the wave passage and incoherence effects, of ground motion on the seismic response of a train-track-bridge system (TTBS). The train is modeled as rigid bodies connected by suspensions, and the track and bridge are modeled as finite elements. The rigid wheel/rail contact is considered, and the coupled equation-of-motion of the TTBS is derived. The power spectrum density (PSD) matrix of ground accelerations is established based on the coherency model, and the PSD matrix is then decomposed to construct a series of pseudo-excitations. The PSD of the pseudo-response of the TTBS under pseudo-excitations is used to calculate the standard deviation. In the numerical example, the seismic responses of a 20-span simply supported bridge under a high-speed train are evaluated by the lateral accelerations of the train and bridge. The results show that the incoherence effect is very important to the seismic responses of TTBS. Furthermore, an earthquake with a faster apparent wave speed and a larger peak acceleration can significantly increase the lateral accelerations of the TTBS.
Keywords:
High-speed train, Railway bridge, Pseudo-excitation method (PEM), Earthquake, Dynamics, Wave passage effect, Incoherence effect키워드:
고속열차, 철도 교량, 유사가진법(PEM), 지진, 동적 응답, 전파통과 효과, 비간섭 효과1. 서 론
고속철도는 큰 수송력, 빠른 속도, 높은 보안성을 가지며 기후 조건의 영향을 적게 받기 때문에 세계적으로 빠르게 발전하고 있다. 새로 건설되는 고속철도의 선로들은 종종 원활하고 안정적인 상태의 궤도와 함께 교량 구조물 위에 설치되고 있다. 이러한 열차-궤도-교량 시스템(train-track-bridge system, TTBS)의 동적 응답은 지난 수십 년 동안 많은 연구자의 관심을 끌어왔다. Xia et al.[1]은 TTBS에 대한 3차원 유한요소 모델을 구축하여 열차와 현수교 간의 동적 상호작용을 조사했다. Dimitrakopoulos and Zeng[2]은 차량-교량 상호작용 축소법을 사용하여 곡선교와 고속열차 간의 상호작용을 해석했다. Salcher and Adam[3]은 TTBS의 동적 상호작용에 대한 궤도 틀림(track irregularity)의 영향을 고려하기 위하여 하부구조 접근법을 사용했다. Hwang et al.[4]은 열차 하중에 대한 3개의 강 박스형 거더교의 동적 응답을 조사하고 교량의 가속도를 감소시킬 수 있는 적절한 방법을 제안했다. 한편, 고속철도는 보통 많은 교량 위를 주행하므로 지진 발생 시 열차가 교량 위에 있을 가능성이 크다. 지진은 구조물의 안전에 강력한 위협이 될 수 있으므로[5],[6], 안전을 보장받기 위해서는 지진에 대한 TTBS의 동적 응답에 대해 더 많은 연구가 필요하다.
궤도 틀림이나 지진과 같이 TTBS에 작용하는 주요 가진(excitation)들은 본질적으로 랜덤(random)하므로, TTBS의 동적 응답 해석을 위해서는 랜덤 진동 이론을 사용해야 한다. 대부분의 기존 연구에서는 TTBS의 동적 응답을 얻기 위한 궤도 틀림이나 지진의 시간이력 표본을 생성하는 데에 몬테카를로법(Monte-Carlo method)을 사용해 왔다[7]. 그러나 몬테카를로법의 정밀도와 신뢰성은 선택하는 표본의 품질과 개수에 크게 의존한다. 많은 표본의 사용은 비효율적인 계산 작업을 발생시키며 때로는 공학 실무에서 구현할 수 없다. 한편, 유사가진법(pseudo-excitation method, PEM)은 구조물의 랜덤 진동 해석에 대한 많은 응용 분야에서 널리 사용되고 있으며, 정상(stationary) 및 비정상(non-stationary) 랜덤 가진을 받는 시간종속 시스템을 효율적이고 정확하게 해석할 수 있다. Li et al.[8]은 PEM을 확장하여 궤도 틀림을 고려한 3경간 교량을 주행하는 열차의 랜덤 진동 거동을 연구했다. Bai et al.[9]은 PEM에 기초해 개발한 수치계산법을 제안하여 바람에 의한 여러 가지 구조물들의 응답에 대해 수치 예측을 제시했다. Jiao et al.[10]은 PEM에 기초하여 등분포 공간변이 정상 가진에 대한 장경간 유연구조물의 확률 응답 계산을 제시했다.
기존의 많은 연구들[11]은 지반 운동의 공간변이가 교량의 지진응답에 중대한 영향을 미친다는 점을 강조해 왔다. 그러나 TTBS에 대한 대부분의 연구들은 단지 각 교량 받침에 도달하는 지진 사이의 시간지연만을 고려했다[12]. 본 연구에서는 PEM을 확장해서, 전파통과 효과나 비간섭 효과와 같은 지반 운동의 공간적 효과들이 조합되어 TTBS의 지진응답에 미치는 영향을 조사한다. 먼저, 간섭 모델에 기초하여, 공간적 효과들을 고려하는 지반 가속도의 파워 스펙트럼(power spectral density, PSD) 행렬을 구성한다. 이를 한 행렬과 그것의 전치행렬의 곱으로 분해하여, 일련의 조화하중, 즉 유사가진(pseudo-excitation)을 구축한다. 그 후 TTBS의 운동방정식을 풀어 랜덤 지진응답의 PSD를 얻는다. 마지막으로 응답들의 표준편차들을 구한다. 중국의 파이어니어(Pioneer) 열차가 주행하는 20경간 단순교에 대한 해석을 통해, 지진의 비간섭 효과, 지진파의 겉보기 속도, 지진 강도 및 열차 속도가 TTBS의 동적 응답에 미치는 영향을 자세히 조사한다.
2. 열차-궤도-교량 시스템(TTBS) 모델
2.1 열차 모델
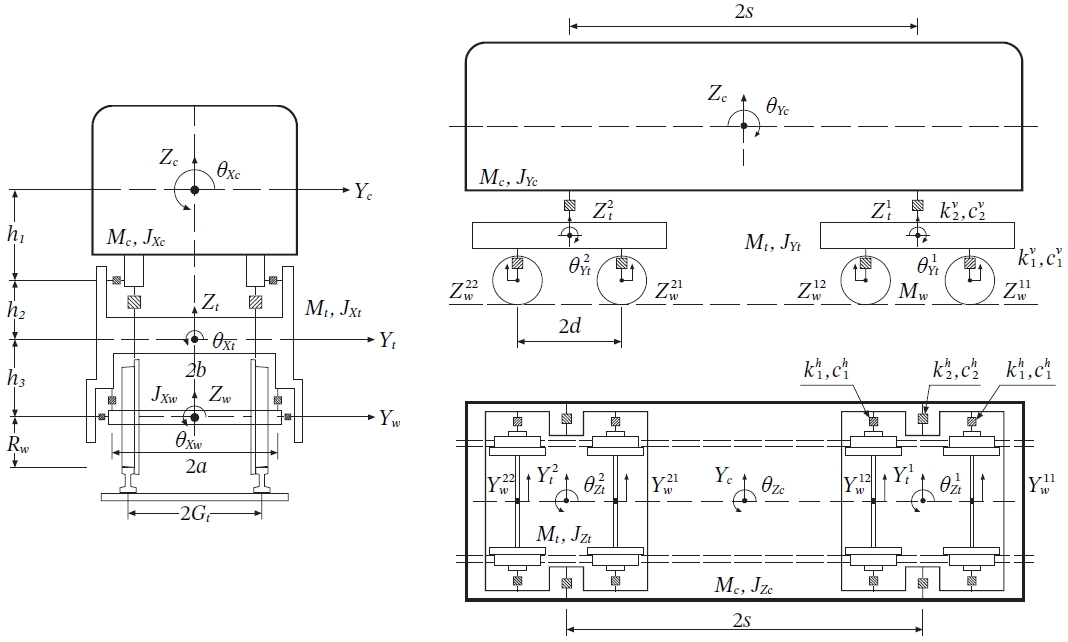
열차의 각 차량 모델은 Fig. 1과 같이 27개의 자유도(degree-of-freedom, DOF)를 가지는 독립적인 질량-완충기-제진기 시스템으로 구축한다[13]. 여기서, Y, Z, θ, φ, ψ는 각각 측면(lateral), 수직(vertical), 횡요(rolling), 종요(pitching) 및 선수요(yawing) 방향의 자유도이고, M과 J는 각각 차량의 질량 및 회전 관성모멘트이며, 아래 첨자 c, t, w는 각각 차체, 대차틀 및 윤축을 의미한다. Gt는 궤간의 절반, a는 윤축에 있는 두 개의 1차 현가장치 사이 수평거리의 절반, b는 각 대차틀에 있는 두 개의 2차 현가장치 사이 수평거리의 절반, d는 각 대차틀에 앞뒤로 있는 바퀴 중심 사이 수평거리의 절반, s는 전방 대차틀의 2차 현가장치와 후방 대차틀의 2차 현가장치 사이 수평거리의 절반을 나타낸다. Rw는 차륜의 반지름, h1은 차체 중앙과 2차 현가장치 사이의 수직거리, h2는 2차 현가장치와 대차틀 중앙 사이의 수직거리, h3은 대차틀 중앙과 1차 현가장치 사이의 수직거리를 나타낸다.
열차의 운동방정식은 다음과 같다.
| (1) |
여기서, M, C, K는 각각 질량, 감쇠 및 강성 행렬이고, u, , 는 각각 거리, 속도 및 가속도 벡터이다. 아래 첨자 w와 v는 각각 열차 차량의 윤축과 기타 부분을 의미하며, Fd는 윤축 중앙에서의 차륜과 궤도 사이 동적 접촉력이다.
2.2 궤도-교량 모델
Fig. 2는 단순 거더교의 유한요소 모델을 보여 준다[14]. 궤도와 교량의 운동방정식은 다음과 같다.
| (2) |
여기서, 아래 첨자 S는 궤도-교량 구조물을 의미한다. Φ, Φb, Φr는 각각 궤도-교량 구조물 전체와 각 교량 및 궤도의 모드형상 행렬, q는 일반화된 좌표이다. N은 궤도 요소의 3차 에르미트(Hermite) 보간행렬, Γ는 윤축 중앙으로부터 양 차륜 끝까지의 변위에 대한 변환행렬이다. Fg는 교량에 작용하는 지진 하중, Fw는 열차 자중에 의한 정상 접촉력이다.
2.3 궤도와 차륜 사이의 직접 접촉
윤축의 운동은 궤도의 운동과 틀림(irregularity)에 따라 달라지므로 운동구속(motion constraint)[13]이라고도 하며, 다음과 같다.
| (3) |
| (4) |
| (5) |
여기서, vt는 열차 속도, r은 궤도 틀림이며, 열차 가속도는 고려하지 않는다.
2.4 열차-궤도-교량 시스템(TTBS)의 운동방정식
식 (3)-(5)를 식 (1)에 대입하여 윤축의 자유도(uw)를 궤도-교량 구조물의 자유도(q)와 궤도 틀림(r)으로 대체한다. 이 새로운 식 (1)을 Fd 항에 대해 정리한 후, 식 (2)에 대입한다. 이렇게 변형된 식 (1)의 첫 번째 행과 식 (2)를 결합하면, 다음과 같은 TTBS의 운동방정식을 얻을 수 있다.
| (6) |
여기서,
질량, 감쇠, 강성 행렬들은 모두 시간에 대해 독립적이며, 뉴마크베타법(Newmark-beta method) 또는 기타 시간적분법으로 풀 수 있다.
3. 유사가진법(PEM)
3.1 실제 가진
TTBS의 운동방정식은 다음과 같이 간단하게 표현된다.
| (7) |
여기서, TTBS의 실제 응답 X(t), , 는 오직 열차 자중에 의해서만 발생하며, 아래의 식을 시간에 대해 적분하여 구할 수 있다.
| (8) |
3.2 정상 랜덤 가진
궤도 틀림에 의해서 발생하는 TTBS의 유사응답 는 아래의 식을 시간에 대해 적분하여 구할 수 있다.
| (9) |
여기서,
| (10) |
| (11) |
ωU와 ωL은 각각 상한 및 하한 차단진동수이고, Nω는 진동수의 표본 개수이다.
PEM의 기본 이론에 따르면[15], 진동수 ωn에서의 궤도 틀림에 의한 유사가진은 다음과 같다.
| (12) |
여기서,
| (13) |
| (14) |
Sa, Sv, Sc는 각각 궤도 틀림의 선형(alignment), 수직(vertical) 및 수준(cross level) 스펙트럼으로서, 그 값들은 미연방 철도국(Federal Railroad Administration[FRA])이 제안한 궤도 틀림의 PSD를 참고했다[16]. Nw는 윤축의 개수이고, τwl(l = 1, 2, ⋯, Nw)은 궤도 위의 어느 한 위치를 첫 번째 윤축이 통과한 후 같은 위치를 l번째 윤축이 통과할 때까지의 시간지연이다.
3.3 비정상 랜덤 가진
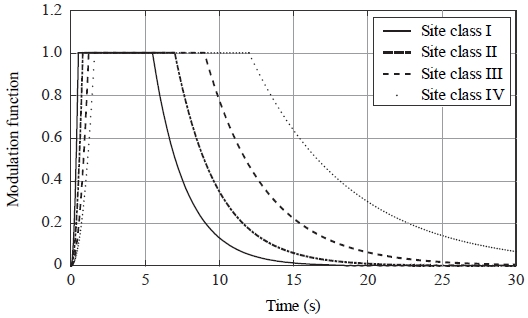
지진의 시간에 따른 변화는 보통 아래와 같은 변조함수(modulation function)로 나타낸다[17].
| (15) |
Table 1은 변조함수의 매개변수(parameter)들이며, Fig. 3은 각 지반 등급(site class)에 대한 변조함수들이다.
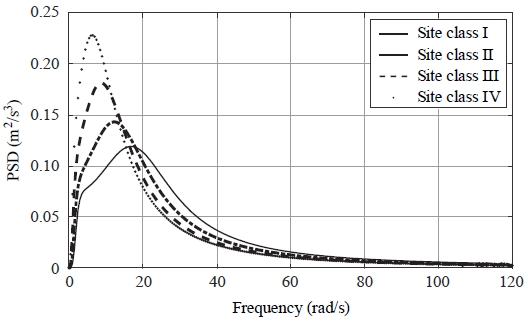
지진의 정상 확률과정은 보통 본 연구에서도 사용한 클러프-펜진(Clough-Penzien) 스펙트럼 Sg(ω)로 설명되며, 그 식은 다음과 같이 정의된다[18].
| (16) |
여기서, ωg와 ζg는 각각 지반의 지배진동수 및 감쇠비이고, ωf와 ζf는 주로 지진 가속도의 저주파 성분을 조절하는 두 번째 필터에 대한 매개변수로서 보통 0.1ωg ≤ ωf ≤ 0.2 ωg, ζf = ζg이다. S0은 분광 강도(spectral intensity)로서 아래와 같다[18].
| (17) |
여기서, 는 최대 지반 가속도와 관련된 매개변수로서, 그 값은 진도 IV, V, VI, VII, VIII, IX에 대해 각각 0.0125g, 0.025g, 0.05g, 0.1g, 0.2g, 0.4g이다. γ는 파고율(peak value factor)이다.
Table 2는 지진 유형 2에 대한 철도공학 내진설계 규정(GB50111-2006)[19] 및 변조함수에 따라 계산된 PSD 함수의 매개변수들이다. Fig. 4는 각 지반 등급에 대한 진도 VII의 클러프-펜진 스펙트럼을 보여 준다. 지반 등급 I이 가장 견고한 지반이고, 지반 등급 IV가 가장 연약한 지반이다.
다지점 지반 운동은 비정상 확률과정으로 가정한다. 교량 받침(지점)에서의 지반 가속도 벡터는 다음과 같다.
| (18) |
파면(wavefront)은 시간 τs1, τs2, ⋯, τsNs에서 교량 받침에 도달한다. i번째 받침에서의 지진 가속도에 대한 비정상 PSD 함수는 다음과 같다.
| (19) |
i번째와 j번째 받침에서의 지진 가속도에 대한 두 받침의 공간변이성은 다음과 같이 상호 파워 스펙트럼(cross-power spectral density, CPSD) 함수로 나타낸다[20].
| (20) |
여기서, 는 지반을 통과하는 지진파의 반사와 굴절에 의한 비간섭 효과(incoherence effect)이고, 는 각 교량 받침에 도달하는 지진파의 시간 차이로 인한 전파통과 효과(wave passage effect)로서 아래와 같다[21].
| (21) |
Harichandran and Vanmarcke[22]는 비간섭 효과를 고려하기 위하여 다음과 같은 H-V 모델을 제안했다.
| (22) |
여기서, dij는 두 교량 받침 사이의 수평거리이고, A와 α는 상수인 매개변수로서 A = 0.736, α = 0.147의 값이 사용된다. θ(ω)는 진동수에 따른 파동의 상관관계 거리로서 아래와 같다.
| (23) |
여기서, K와 b는 상수인 매개변수로서 K = 5,210, b = 2.78의 값이 사용된다. ω0은 “절점진동수”로서 ω0 = 6.58 rad/s의 값이 사용되며, ω는 원진동수(각속도)로서 역시 rad/s의 단위를 사용한다.
PSD 행렬의 성분에 대한 상기 식들에 따라, 모든 교량 받침들에 대한 PSD 행렬을 다음과 같이 표현할 수 있다.
| (24) |
PSD 행렬 는 양의 정부호 에르미트 행렬로서 아래와 같이 분해할 수 있다.
| (25) |
여기서, “*”은 켤레 복소수를 의미하며,
| (26) |
| (27) |
| (28) |
T는 양의 정부호 실수 대칭행렬로서 아래와 같이 하삼각행렬 Q와 전치행렬의 곱으로 분해할 수 있다.
| (29) |
따라서, PSD 행렬 는 다음과 같이 표현할 수 있다.
| (30) |
여기서,
| (31) |
PEM의 이론에 기초하여, 지반의 유사가속도 유사속도 , 유사변위 는 아래와 같이 표현할 수 있다.
| (32) |
상대운동법[23]은 구조물에 작용하는 다지점 지진 하중을 다루는 데에 널리 사용되는 방법이다. 오직 지진만을 고려한 TTBS의 운동방정식은 다음과 같이 간단하게 표현된다.
| (33) |
여기서, m은 교량 받침의 자유도이고, Fe는 지진에 의해 발생하는 반력 벡터이다. TTBS의 전체 변위는 다음과 같이 표현할 수 있다.
| (34) |
여기서, 위 첨자 p와 d는 각각 정적 유사변위와 동적 응답변위를 의미한다.
TTBS의 정적 유사변위는 다음과 같다.
| (35) |
여기서,
| (36a) |
| (36b) |
식 (34)와 식 (35)를 식 (33)의 첫 두 행에 대입하고, 지진 하중의 감쇠 부분을 무시하면 다음과 같은 식을 얻는다.
| (37) |
식 (32)를 식 (36)에 대입하면 아래와 같이 지반의 유사변위에 대한 궤도와 교량의 정적 유사응답을 구할 수 있다.
| (38) |
동적 유사지진은 다음과 같다.
| (39) |
지진에 의한 TTBS의 동적 유사응답 는 아래 식을 시간에 대해 적분하여 구할 수 있다.
| (40) |
지진 하중에 대한 TTBS의 전체 유사응답은 다음과 같다.
| (41) |
시간 tk에서 궤도 틀림에 의한 TTBS의 유사응답들을 다음과 같이 가정한다.
| (42) |
그러면 의 PSD는 아래와 같다.
| (43) |
시간 tk에서 지진에 의한 TTBS의 유사응답들을 다음과 같이 가정한다.
| (44) |
그러면 의 PSD는 아래와 같다[24].
| (45) |
유사응답 의 표준편차는 다음과 같다.
| (46) |
4. 수치 예제
Fig. 5는 본 사례 연구에서 사용한 중국의 파이어니어 열차 및 20경간 교량 모델을 보여 준다. 열차에는 4대의 견인차(tractor)와 2대의 부수차(trailer)가 있으며 각 교량 경간은 24 m이다. 열차와 각 경간의 교량 상판(deck) 및 각 교각(pier)이 가지는 속성은 Choi and Mu[13]를, 철도(rail)와 체결장치(fastener)의 속성은 Zeng et al.[25]을 참고했다.
각 단계의 시간증분은 0.001초로 설정한다. PEM에는 궤도-교량 구조물의 첫 300개의 진동 모드와 가진의 200개의 진동수를 고려한다. 궤도 틀림의 스펙트럼은 FRA가 분류한 6개의 등급 중 제6등급을 고려한다[16]. 열차가 속도 v로 교량에 진입하면 진도 VI의 측면 방향 지진 가속도가 왼쪽에서 첫 번째 교각에 도달하고 오른쪽으로 전파된다. 모든 경우에 대해서 Table 1의 지반 등급 I을 고려한다.
4.1 비간섭 효과의 영향
지반 상태의 비간섭 효과가 TTBS의 동적 응답에 미치는 영향을 조사하기 위하여, 500 m/s와 무한대인 지진파의 겉보기 속도에 대해 비간섭 효과를 고려하는 해석과 고려하지 않는 해석을 수행한다. 열차 속도는 300 km/h로 설정한다. Fig. 6(a)와 6(b)는 각각 두 지진파 속도와 비간섭 효과의 고려 유무에 따라서 각 차체와 교량 경간에 발생하는 측면 가속도들의 최대 표준편차들을 보여 준다.
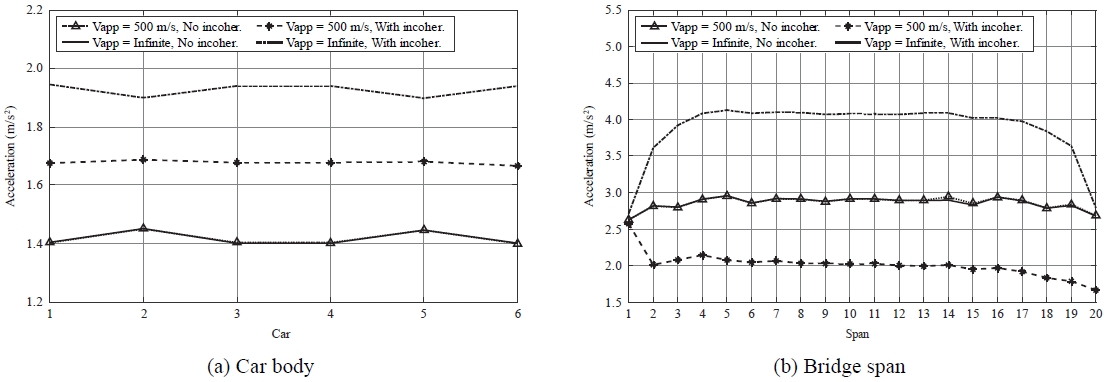
Maximum standard deviation of the lateral acceleration of each (a) car body and (b) bridge span with different wave speed and incoherence effect
본 예제의 총길이가 480 m인 20경간 교량의 경우, 비간섭 효과를 고려하지 않으면, 열차와 교량의 측면 가속도는 지진파 속도가 달라져도 거의 변화가 없다. 비간섭 효과를 고려한 경우와 비교하면, 열차의 측면 가속도는 지진파 속도가 500 m/s와 무한대일 때 각각 15 %와 27 % 작게 산출된다. 한편, 교량 경간의 측면 가속도는 지진파 속도가 각각 500 m/s일 때 42 % 크게, 무한대일 때 26 % 작게 산출된다. 여기서, 수치값은 각 해석값의 평균값으로 계산했다. 따라서, 지진의 비간섭 효과를 고려하지 않으면 TTBS의 동적 응답이 부적절하게 추정될 것이다.
4.2 지진파 속도의 영향
지진파의 겉보기 속도가 TTBS의 동적 응답에 미치는 영향을 조사하기 위하여, 전파통과 효과와 비간섭 효과를 모두 포함하고, 지진파의 겉보기 속도를 500 m/s, 1,000 m/s, 1,500m/s, 2,500 m/s, 3,500 m/s 및 무한대로 고려한다. 열차 속도는 300 km/h로 설정한다. Fig. 7(a)와 7(b)는 각각 지진파 속도에 따라서 각 차체와 교량 경간에 발생하는 측면 가속도들의 최대 표준편차들을 보여 준다.
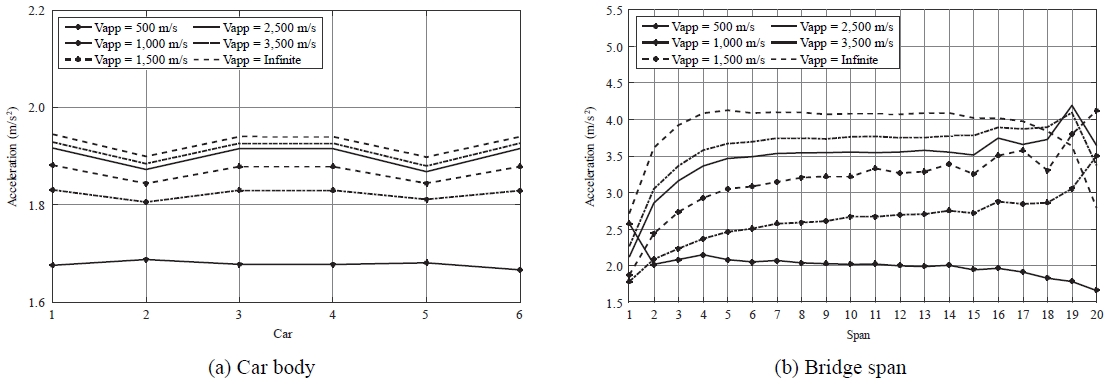
Maximum standard deviation of the lateral acceleration of each (a) car body and (b) bridge span with different earthquake wave speed with incoherence effect
해석 결과로부터 지진파 속도가 빠를수록 열차와 교량의 측면 가속도가 증가하는 것이 분명하게 나타난다. 지진파 속도가 500 m/s와 무한대일 때 측면 가속도 최대 표준편차들의 평균값은, 차체의 경우 각각 1.68 m/s2와 1.93 m/s2이고, 교량 경간의 경우 각각 2.01 m/s2와 3.88 m/s2이다. 즉, 지진파 속도를 고려하지 않으면(무한대로 가정하면) TTBS의 동적 응답, 특히 교량의 동적 응답이 크게 산출되게 된다.
4.3 지진 강도의 영향
지진 강도가 TTBS의 동적 응답에 미치는 영향을 조사하기 위하여, 진도 IV, V, VI, VII, VIII, IX의 지진들을 고려한다. 열차 속도는 200 km/h, 지진파의 겉보기 속도는 1,000 m/s로 설정한다. Fig. 8(a)와 8(b)는 각각 지진 강도에 따라서 각 차체와 교량 경간에 발생하는 측면 가속도들의 최대 표준편차들을 보여 준다.
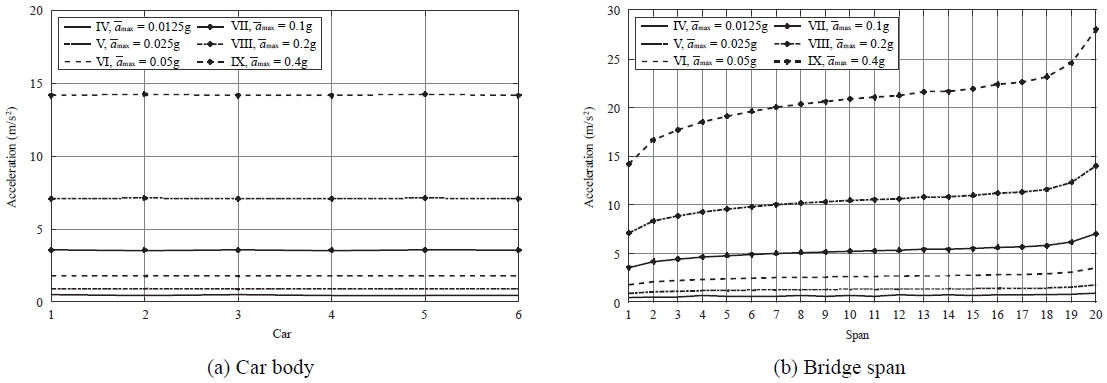
Maximum standard deviation of the lateral acceleration of each (a) car body and (b) bridge span with different seismic intensity with incoherence effect
지반 가속도가 클수록 열차와 교량의 측면 가속도 또한 매우 증가한다. 각 진도에 따른 최대 지반 가속도 매개변수 āmax에 대한 측면 가속도 표준편차들의 평균값을 āmax로 나눈 값은, 차체의 경우 약 3.6 선에 머물러 있으며, 교량 경간의 경우 5.3을 유지한다. 즉, 열차 차체와 교량 경간의 측면 가속도 표준편차는 최대 지진 가속도에 거의 비례한다.
4.4 열차 속도의 영향
열차 속도가 TTBS의 동적 응답에 미치는 영향을 조사하기 위하여, 열차 속도를 200 km/h, 240 km/h, 280 km/h, 320 km/h, 360 km/h, 400 km/h로 고려한다. 지진파의 겉보기 속도는 1,000 m/s로 설정한다. Fig. 9(a)와 9(b)는 각각 열차 속도에 따라서 각 차체와 교량 경간에 발생하는 측면 가속도들의 최대 표준편차들을 보여 준다.
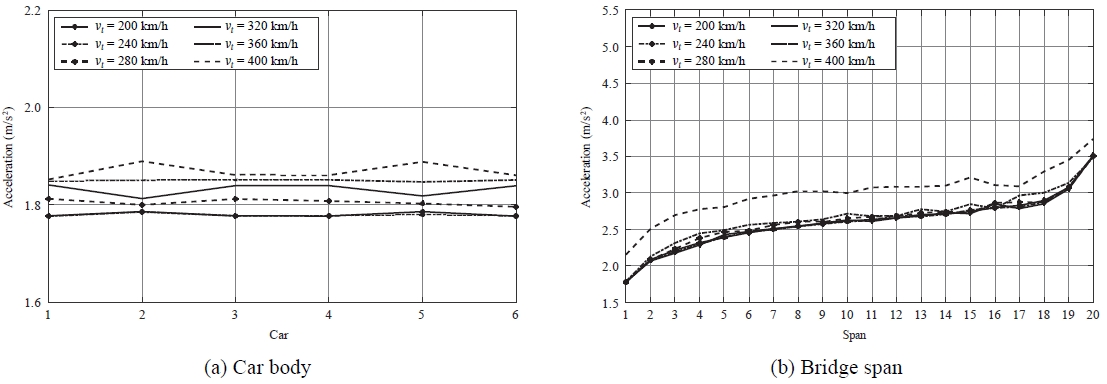
Maximum standard deviation of the lateral acceleration of each (a) car body and (b) bridge span with different train speed with incoherence effect
열차 속도가 200 km/h에서 360 km/h로 빨라지면, 열차와 교량의 측면 가속도는 각각 4 % 및 3 % 정도 약간 증가한다. 그런데 열차 속도가 400 km/h가 되면, 200 km/h일 때에 비해서 열차의 측면 가속도는 단지 5 %만 증가하는 데에 반해, 교량의 측면 가속도는 16 %나 증가한다. 이는 열차 속도가 400 km/h일 때, 열차 하중이 교량에 발생시킨 진동이 교량의 측면 진동을 공진 상태에 이르게 했을 것으로 추정된다. 즉, 이렇게 일부 열차 속도에서 교량이 공진 상태가 되는 경우를 제외하면, 열차와 교량의 측면 가속도는 주로 열차 속도보다 지진으로부터 영향을 받는다.
5. 결 론
본 연구에서는 지진의 공간변이에 의한 전파통과 효과와 비간섭 효과를 고려하여 TTBS의 지진응답 해석을 수행할 수 있는 효율적인 랜덤 알고리즘을 개발했다. 각 교량 받침에 도달하는 비정상 랜덤 지진들을 PSD 행렬로 구성한 후, 이를 분해하여 유사가진을 구축했다. 본 연구의 결론을 정리하면 다음과 같다.
- (1) PEM은 랜덤 가진의 수많은 시간이력들을 생성하기 위하여 많은 시간을 소모해야 하는 절차를 요구하지 않으며, 랜덤 가진의 PSD로부터 동적 응답들의 표준편차들을 직접 산출할 수 있다.
- (2) TTBS에 흔히 사용되는 다경간 단순철도교에 대해서, 지진의 비간섭 효과는 열차와 교량 모두의 측면 가속도에 전파통과 효과보다 훨씬 더 큰 영향을 미치기 때문에 무시해서는 안 된다.
- (3) 지진파의 겉보기 속도가 빠를수록 TTBS의 측면 가속도, 특히 교량의 측면 가속도가 크게 증가할 수 있다.
- (4) 지진의 최대 가속도가 TTBS의 동적 응답을 지배한다. TTBS의 측면 가속도는 지진의 최대 가속도를 따라서 선형으로 증가한다.
- (5) 열차와 교량 사이에 공진 현상이 발생하지 않는 한, 열차 속도의 변화는 지진의 영향에 비해 TTBS의 측면 가속도에 큰 영향을 미치지 않는다.
References
-
Xia, H., Xu, Y.L., and Chan, T.H.T. (2000) Dynamic Interaction of Long Suspension Bridges with Running Trains, Journal of Sound and Vibration, Elsevier, Vol.237, No.2, pp.263-280.
[https://doi.org/10.1006/jsvi.2000.3027]

-
Dimitrakopoulos, E.G., and Zeng, Q. (2015) A Three-Dimensional Dynamic Analysis Scheme for the Interaction Between Trains and Curved Railway Bridges, Computers & Structures, Elsevier, Vol.149, pp.43-60.
[https://doi.org/10.1016/j.compstruc.2014.12.002]

-
Salcher, P., and Adam, C. (2015) Modeling of Dynamic Train-Bridge Interaction in High-Speed Railways, Acta Mechanica, Springer, Vol.226, No.8, pp.2473-2495.
[https://doi.org/10.1007/s00707-015-1314-6]

- Hwang, E.S., Kim, D.Y., and Jang, S.H. (2017) Analysis of Dynamic Response and Vibration Mitigation for Steel Box Girder Railway Bridges, Journal of Korean Society of Steel Construction, KSSC, Vol.29, No.6, pp.487-495 (in Korean).
- Han, S.W., Kim, T.O., and Ha, S.J. (2017) Seismic Performance Evaluation of Special Moment Steel Frames with Torsional Irregularities - I Seismic Design, Journal of Korean Society of Steel Construction, KSSC, Vol.29, No.5, pp.361-368 (in Korean).
- Han, S.W., and Kim, T.O. (2017) Seismic Performance Evaluation of Special Moment Steel Frames with Torsional Irregularities - II Improving Seismic Design Method, Journal of Korean Society of Steel Construction, KSSC, Vol.29, No.5, pp.369-376 (in Korean).
-
Rocha, J.M., Henriques, A.A., and Calçada, R. (2014) Probabilistic Safety Assessment of a Short Span High-Speed Railway Bridge, Engineering Structures, Elsevier, Vol.71, pp.99-111.
[https://doi.org/10.1016/j.engstruct.2014.04.018]

-
Li, X., Zhu, Y., and Jin, Z. (2016) Nonstationary Random Vibration Performance of Train-Bridge Coupling System with Vertical Track Irregularity, Shock and Vibration, Hindawi, Vol.2016, 1450895.
[https://doi.org/10.1155/2016/1450895]

-
Bai, Y., Zhang, Y., Liu, T., Kennedy, D., and Williams, F. (2019) Numerical Predictions of Wind-Induced Buffeting Vibration for Structures by a Developed Pseudo-Excitation Method, Journal of Low Frequency Noise, Vibration and Active Control, Sage, Vol.38, No.2, pp.510-526.
[https://doi.org/10.1177/1461348419828248]

-
Jiao, C.-K., Dong, X., Li, A.-Q., Zhou, G.-D., and Wu, X.-P. (2017) Seismic Response of Long-Span Triple-Tower Suspension Bridge Under Random Ground Motion, Mathematical Problems in Engineering, Hindawi, Vol.2017, 3457452.
[https://doi.org/10.1155/2017/3457452]

-
Bi, K., Hao, H., and Chouw, N. (2011) Influence of Ground Motion Spatial Variation, Site Condition and SSI on the Required Separation Distances of Bridge Structures to Avoid Seismic Pounding, Earthquake Engineering & Structural Dynamics, John Wiley & Sons, Vol.40, No.9, pp.1027-1043.
[https://doi.org/10.1002/eqe.1076]

-
Zhang, N., Xia, H., and De Roeck, G. (2010) Dynamic Analysis of a Train-Bridge System Under Multi-Support Seismic Excitations, Journal of Mechanical Science and Technology, Springer, Vol.24, No.11, pp.2181-2188.
[https://doi.org/10.1007/s12206-010-0812-7]

- Choi, D.-H., and Mu, D. (2018) Running Safety of a High-Speed Train Through a Multi-Span Bridge Under a Non-Uniform Moderate Earthquake, Proceedings of the 40th IABSE Symposium: Tomorrow’s Megastructures, International Association for Bridge and Structural Engineering, France, pp.S20-59-S20-66.
- Choi, D.-H., Mu, D., Ma, C., Park, M.-W., and Lim, J.-H. (2019) Random Analysis of the Safety of a High-Speed Train through a Bridge Under Earthquake, Proceedings of the 20th IABSE Congress: The Evolving Metropolis, International Association for Bridge and Structural Engineering, USA, pp.2056-2063.
-
Lu, F., Lin, J.H., Kennedy, D., and Williams, F.W. (2009) An Algorithm to Study Non-Stationary Random Vibrations of Vehicle-Bridge Systems, Computers & Structures, Elsevier, Vol.87, No.3, pp.177-185.
[https://doi.org/10.1016/j.compstruc.2008.10.004]

- Cooperrider, N.K., Law, E.H., Hull, R., Kadala, P.S., and Tuten, J.M. (1975) Analytical and Experimental Determination of Wheel-Rail Constraint Relationships, Report No. FRA-OR&D-76-244, Federal Railroad Administration (U.S. Department of Transportation).
-
Lin, J.H., Sun, D.K., Sun, Y., and Williams, F.W. (1997) Structural Responses to Non-Uniformly Modulated Evolutionary Random Seismic Excitations, Communications in Numerical Methods in Engineering, John Wiley & Sons, Vol.13, No.8, pp.605-616.
[https://doi.org/10.1002/(SICI)1099-0887(199708)13:8<605::AID-CNM75>3.0.CO;2-I]

-
Chen, J., Kong, F., and Peng, Y. (2017) A Stochastic Harmonic Function Representation for Non-Stationary Stochastic Processes, Mechanical Systems and Signal Processing, Elsevier, Vol.96, pp.31-44.
[https://doi.org/10.1016/j.ymssp.2017.03.048]

- Ministry of Construction, and General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China (2009) Code for Seismic Design of Railway Engineering (GB50111-2006), China (in Chinese).
-
Zhang, Y.H., Li, Q.S., Lin, J.H., and Williams, F.W. (2009) Random Vibration Analysis of Long-Span Structures Subjected to Spatially Varying Ground Motions, Soil Dynamics and Earthquake Engineering, Elsevier, Vol.29, No.4, pp.620-629.
[https://doi.org/10.1016/j.soildyn.2008.06.007]

-
Lin, J., Zhang, Y., and Yan, Z. (2005) Seismic Spatial Effects on Long-Span Bridge Response in Nonstationary Inhomogeneous Random Fields, Earthquake Engineering and Engineering Vibration, Springer, Vol.4, No.1, pp.75-82.
[https://doi.org/10.1007/s11803-005-0026-7]

-
Harichandran, R.S., and Vanmarcke, E.H. (1986) Stochastic Variation of Earthquake Ground Motion in Space and Time, Journal of Engineering Mechanics, American Society of Civil Engineers, Vol.112, No.2, pp.154-174.
[https://doi.org/10.1061/(ASCE)0733-9399(1986)112:2(154)]

-
Zhu, D.Y., Zhang, Y.H., Kennedy, D., and Williams, F.W. (2014) Stochastic Vibration of the Vehicle-Bridge System Subject to Non-Uniform Ground Motions, Vehicle System Dynamics, Taylor & Francis, Vol.52, No.3, pp.410-428.
[https://doi.org/10.1080/00423114.2014.886707]

-
Jia, H.-Y., Zhang, D.-Y., Zheng, S.-X., Xie, W.-C., and Pandey, M.D. (2013) Local Site Effects on a High-Pier Railway Bridge Under Tridirectional Spatial Excitations: Nonstationary Stochastic Analysis, Soil Dynamics and Earthquake Engineering, Elsevier, Vol.52, pp.55-69.
[https://doi.org/10.1016/j.soildyn.2013.05.001]

-
Zeng, Z.-P., Liu, F.-S., Lu, Z.-H., Yu, Z.-W., Lou, P., and Chen, L.-K. (2016) Three-Dimensional Rail-Bridge Coupling Element of Unequal Lengths for Analyzing Train-Track-Bridge Interaction System, Latin American Journal of Solids and Structures, Associação Brasileira de Ciências Mecânicas, Vol.13, No.13, pp.2490-2528.
[https://doi.org/10.1590/1679-78252551]