실리콘 점성댐퍼의 속도의존성 거동에 대한 실험적 성능 평가
Copyright © 2019 by Korean Society of Steel Construction
초록
본 논문에서는 오일 대신 실리콘 겔이 충진된 점성댐퍼의 성능을 평가하기 위한 실험적 연구가 진행되었다. 제안된 댐퍼의 속도의존적인 특성을 확인하기 위해 0.5 mm/s에서 40 mm/s에 이르는 다양한 속도 하에서 댐퍼에 발생되는 하중을 계측하였으며 그 변화 경향을 분석하였다. 실험 결과, 제안된 실리콘 점성 댐퍼는 댐퍼의 변위 증가와는 무관하게 하중이 일정하게 유지되었으며, 댐퍼의 작동 속도가 증가할수록 축방향 저항력이 비선형적으로 증가하는 특성을 나타냈다. 5회 반복 계측된 댐퍼의 하중, 유효강성 및 에너지 소산량의 평균 대비 편차의 비율은 대부분 2 % 미만으로 계측되어 제안된 댐퍼의 안정적인 거동을 확인할 수 있었다. 또한, 실험 데이터에 근거하여 제안된 댐퍼의 속도에 따른 하중 크기를 정의할 수 있는 관계식을 제안하였다.
Abstract
In this paper, a viscous damper infilled with silicone gel was proposed that can replace conventional oil dampers. A series of experimental tests were conducted to verify the damping performance of the proposed device depending on the operating velocity of the piston rod. Test results showed that the force in the energy-dissipation device was kept constant regardless of the damper displacement and increased nonlinearly as the loading velocity increased. For the damper forces, effective stiffnesses, and energy dissipations measured five times repeatedly at each loading step, the ratios of deviations to average values were less than 2 %, which means that the proposed damper behave stably subject to repeated loading. Additionally, the equation for describing the force-velocity relationships of the device was suggested based on the test results.
Keywords:
Viscosity, Damper, Silicone, Seismic design, Velocity-dependence, Energy dissipation키워드:
점성, 감쇠장치, 실리콘, 내진설계, 속도의존성, 에너지소산1. 서 론
건축물의 내진성능을 향상시키는 방법은 크게 세 가지로, 건축 구조물 자체의 성능(강도/강성/연성)을 증진시키는 방법(내진구조)과 제진장치를 통해 지진하중을 감소시키는 방법(제진구조), 그리고 건축물을 지반으로부터 분리하여 지진력의 전달을 원천 차단하는 방법(면진구조)이 널리 사용된다[1]. 이 중 제진구조에 사용되는 장치는 에너지 소산을 통해 건축물의 감쇠력을 높이는 역할을 하며, 이 에너지 소산 장치의 작동 메카니즘에 따라 점성댐퍼, 마찰댐퍼, 강재이력댐퍼 등으로 그 종류가 구분된다[2],[3].
일반적으로 점성댐퍼는 주로 실리콘 오일과 같은 유체가 에너지 소산 매개체로 사용되며, 작동 속도에 의한 유체 점성이 감쇠력을 발생시킨다[4]. 정적하중 상태에서는 탄성강성이 거의 없고, 속도와 변위의 위상차에 의한 기존 부재의 하중 부담을 줄일 수 있는 것이 주요 특징이다. 또한, 작동 후에도 제품에 손상이 발생하지 않기 때문에 반영구적으로 사용이 가능하며 여진에도 대비할 수 있는 장점이 있다. 이러한 특징 때문에 점성댐퍼는 자동차, 선박 산업 분야는 물론, 건축·토목 분야에서도 감쇠장치로서 널리 활용되고 있다[5]-[8]. 그러나 오일이 담겨있는 실린더는 구조적으로 완전히 밀봉되는 것이 불가능하기 때문에, 오일이 새는 누유 현상이 필연적으로 발생한다(Fig. 1)[9]. 실린더 내 유체가 완전히 충전되어 있지 않을 경우 댐퍼의 성능이 심각히 저하될 수 있는 문제점이 있으며, 유지보수에 주의를 기울여야 하는 단점이 있다.
본 연구에서는 이러한 유지보수 상의 문제점을 해결하고자 오일 대신 겔(gel) 형상의 실리콘을 충전재로 사용한 점성댐퍼를 개발하였으며, 제안된 실리콘 점성댐퍼에 대해 속도의존성 거동을 실험적으로 평가하고자 하였다.
2. 실험 계획
2.1 실험체 형상
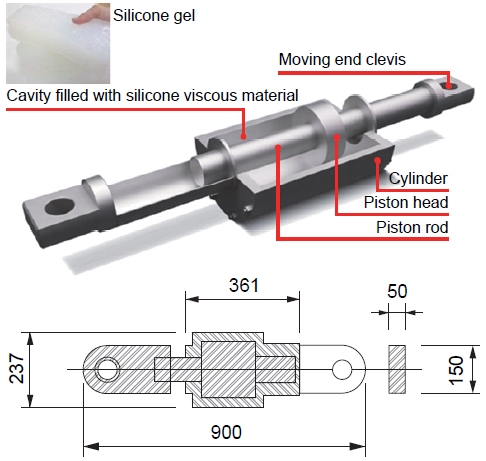
실험에 사용된 실리콘 점성댐퍼의 형상 및 외관 치수를 Fig. 2에 나타냈다. Fig. 2에 나타낸 바와 같이, 본 점성댐퍼는 실리콘 겔이 채워진 원기둥 형상의 실린더(cylinder)와 실리콘 겔에 하중을 전달하기 위한 피스톤부(piston rod & piston head) 및 본 댐퍼를 구조체에 핀으로 접합하기 위한 클레비스(clevis)로 구성된다. 본 점성댐퍼 역시 여타 다른 유체 점성댐퍼들과 마찬가지로, 피스톤 헤드와 실린더 사이에 형성된 틈(orifice)으로 내부 충진 물질인 실리콘 겔이 이동하면서 감쇠력을 발생시킨다.
내부에 충진되는 실리콘 겔의 경우, 반투명한 색상을 띄며 그 비중은 약 1.13이다. 해당 소재의 점성(viscosity)을 확인하기 위해 회전형 레오미터를 이용하여 상온에서의 점도를 계측하였다. 그 결과 1 Hz에서 25,083 Pa·s를 나타냈으며 주파수가 증가할수록 선형적으로 감소하여 10 Hz에서는 4,130 Pa·s를 나타냈다.
2.2 실험 셋업
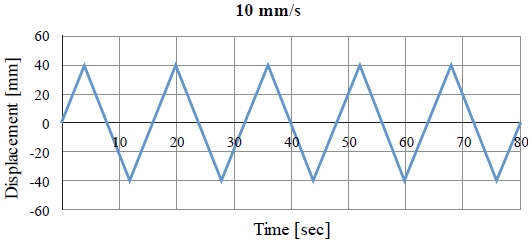
실험은 명지대학교 하이브리드구조실험센터에서 진행하였으며, Fig. 3과 같이 본 점성댐퍼를 5,000 kN 용량의 universal testing machine(UTM)에 설치하고 축방향으로 가력을 실시하였다. 가력 속도는 실험에 사용된 UTM의 최대가용 속도 40 mm/s를 고려하여 설정하였으며, 본 점성댐퍼가 속도의존적인 특성을 가지고 있는 만큼 다양한 속도 범위(0.5 mm/s, 1 mm/s, 2 mm/s, 3 mm/s, 5 mm/s, 10 mm/s, 15 mm/s, 20 mm/s, 30 mm/s, 40 mm/s) 내에서 해당 장치의 성능을 확인하고자 하였다. 가력 방식은 KBC 2016 0306.13.6에 근거하여 매 속도에 대해 5회 반복실험을 하였으며[10], 가력 프로토콜은 Fig. 4와 같이 삼각파 형태로 가력하는 동안 속도가 일정하게 유지되도록 하였다. 또한, 최대 가력 변위는 장치원형의 최대 가용 스트로크에 맞추어 ±40 mm로 하였다. 실험 당일 주변 온도는 21.5 ℃ ± 0.1 ℃, 습도는 89 % ± 1 % R.H.이었다.
3. 실험 결과
3.1 감쇠장치의 하중-변위 관계
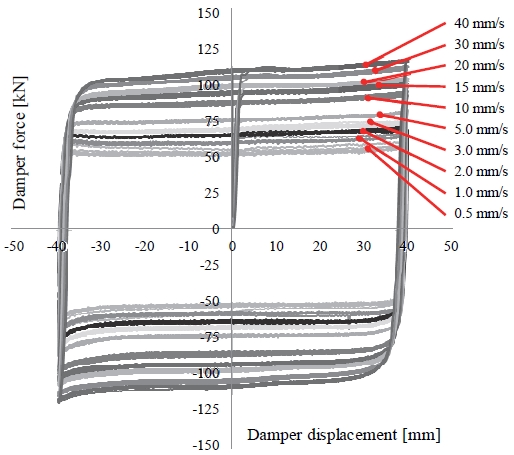
Fig. 5는 다양한 가력 속도 하에서의 실리콘 점성댐퍼의 하중-변위 곡선을 나타낸 것이다. 해당 그림에서 확인해 볼 수 있듯이, 제안된 댐퍼는 댐퍼에 발생하는 변위 증가와는 무관하게 축방향으로 발생하는 저항력이 일정하게 유지되었으며, 댐퍼에 가해지는 가력 속도가 증가할수록 그 저항력은 증가하는 특성을 나타냈다. 한편, 제작된 댐퍼는 실험 종료 시점까지 실리콘 누출 없이 안정적인 거동을 나타냈다.
3.2 제로 변위에서의 하중, F0
Table 1에 실험으로부터 계측된 변위 0지점에서의 댐퍼 하중의 크기를 사이클별로 정리하여 나타냈다. 제안된 감쇠장치의 적합성을 평가하기 위해 정·부방향에 대한 하중 크기를 각각 나타냈으며, 해당 항목별로 평균을 산정하여 식 (1)과 같이 이에 대한 편차비율을 퍼센트 값(σ)으로 나타냈다.
| (1) |
여기서, F0+와 F0–는 각각 정·부방향 제로 변위에서의 하중을 나타내며, F0, Avg.는 제로변위에서 5회 반복 계측된 하중들의 평균값을 나타낸다.
가력 속도가 0.5 mm/s일 경우, 정·부방향에 대한 하중의 크기는 평균 53.6 kN, -53.5 kN을 각각 나타냈으며, 해당 속도에서 평균에 대한 편차 최대비율은 7.6 %로 KBC 2016에서 제시하고 있는 15 % 기준보다 작게 측정되었다[10].
가력 속도 1.0 mm/s에서 계측된 정·부방향에 대한 하중의 크기는 60.1 kN과 -58.3 kN으로 0.5 mm/s에 비해 그 저항력의 크기가 평균 10.6 % 증가하였다. 해당 속도에서 확인된 평균 대비 편차 최대비율은 2.6 %였다.
가력 속도 2.0 mm/s에서는 댐퍼 하중의 크기가 0.5 mm/s 대비 평균 21.2 % 증가한 65.6 kN, -64.1 kN을 각각 평균값으로 나타냈다. 평균 대비 편차 최대비율은 1.9 %로 안정적인 이력거동을 확인할 수 있었다.
가력 속도 3.0 mm/s에서 계측된 정·부방향에 대한 하중의 크기는 평균 69.7 kN과 -68.1 kN으로 각각 확인되었으며, 최대 편차비율은 2.0 %였다. 해당 성능은 가력 속도 0.5 mm/s 대비 28.7 %가 증가된 수치이다.
가력 속도를 첫 가력 속도의 10배로 증가시킨 5.0 mm/s에서는 정·부방향에 대한 하중의 크기가 평균 75.8 kN, -73.8 kN으로 확인되었으며, 이는 0.5 mm/s에서의 저항력보다 약 39.7 % 향상된 값이었다. 평균 대비 편차의 최대비율도 1.3 %밖에 되지 않아 안정적인 거동을 확인할 수 있었다.
가력 속도 10 mm/s에서 계측된 정·부방향에 대한 댐퍼 하중의 크기는 평균 88.3 kN, -86.4 kN을 각각 나타냈으며, 편차의 최대 비율은 2.1 %였다. 가력 속도 0.5 mm/s 대비 하중은 63.2 %까지 증진되었다.
가력 속도 15 mm/s에서 정·부방향에 대한 하중 크기는 각각 평균 95.3 kN, -93.6 kN을 나타냈으며, 평균 대비 편차 비율 중 최대값은 1.5 %였다. 본 속도에서의 하중은 초기 계측된 하중값에 비해 평균 76.4 % 증가된 값이다.
댐퍼의 작동 속도가 20 mm/s까지 증가될 경우, 댐퍼의 축방향 저항력의 크기는 약 85 % 증가하여 정·부방향에서 계측된 평균값은 각각 99.6 kN, -98.0 kN을 나타냈다. 본 속도에서 최대 편차 비율은 1.4 %로 매 사이클마다 거동에 큰 차이를 나타내지 않았다.
가력 속도가 30 mm/s일 경우, 정·부방향에 대한 하중의 크기는 평균 106.2 kN, -105.0 kN을 각각 나타냈으며, 해당 실험에서 확인된 평균 대비 편차 최대비율은 1.3 %였다. 본 속도에서는 가력 속도 0.5 mm/s에서 확인된 하중 크기 대비 97.2 % 향상된 저항성능을 나타냈다.
마지막으로 초기 가력 속도보다 80배 속도를 높인 40 mm/s에서는 하중이 약 2배 가까이 증가하였으며, 그 크기는 정·부방향에 대해 평균 110.4 kN, -108.8 kN을 각각 나타냈다. 평균 대비 편차 비율 역시 1.3 % 이하의 높은 신뢰성을 나타내며 이력거동하였다.
추가적으로 모든 가력 스텝에서 반복 가력이 진행될수록 하중이 조금씩 떨어지는 현상이 공통적으로 나타났다. 이는 가력이 진행될수록 내부 실리콘 겔의 온도가 올라가 입자 사이의 결합이 유연해 졌으며, 이로 인해 댐퍼 내부의 실린더 해드와 로드 사이에 형성된 간극으로 실리콘 겔이 보다 쉽게 이동이 가능해졌기 때문이다. 그러나 이러한 현상에 의한 하중 감소는 평균 대비 1 % - 2 % 수준으로 댐퍼 거동의 신뢰성에 영향을 미칠 정도는 아닌 것으로 판단되었다.
3.3 유효 강성, keff
제안된 점성댐퍼의 유효 강성은 식 (2)에 의거하여 결정할 수 있다[10].
| (2) |
여기서, , 는 각각 감쇠장치의 정·부방향으로 발생하는 최대변위(본 실험에서는 ±40 mm)이며, , 는 각각 , 에서 발생하는 감쇠장치의 하중을 나타낸다.
Table 2에 가력 속도별 및 사이클별로 계산된 유효 강성의 크기를 정리하여 나타냈다. 해당 표에서 확인해볼 수 있듯이 가력 속도 0.5 mm/s, 1.0 mm/s, 2.0 mm/s, 3.0 mm/s, 5.0 mm/s, 10 mm/s, 15 mm/s, 20 mm/s, 30 mm/s, 그리고 40 mm/s에서 확인된 유효 강성의 크기는 각각 1.535 kN/mm, 1.696 kN/mm, 1.845 kN/mm, 1.955 kN/mm, 2.112 kN/mm, 2.409 kN/mm, 2.561 kN/mm, 2.653 kN/mm, 2.838 kN/mm, 그리고 2.952 kN/mm로 나타났다. 모든 가력 스텝에서 산출된 평균 대비 편차의 최대 비율은 0.5 %에서 2.0 % 사이에 대부분 분포하였으며, 이를 통해 감쇠 성능에 대한 편차가 크지 않음을 확인할 수 있었다. 다만, 속도 0.5 mm/s에 대해 첫 번째 사이클 유효 강성이 평균과 비교하여 6.5 % 높은 수치를 나타냈는데, 이것은 첫 번째 가력 스텝의 첫 번째 사이클 실험 진행 시 UTM기와 장치원형이 가력 방향으로 재정렬 되는 과정에서 다소 하중이 높게 측정된 것에 그 원인이 있는 것으로 분석되었다.
3.4 에너지 소산량, E
Table 3은 하중-변위 이력곡선 내 면적으로부터 산출된 매 사이클별 에너지 소산량을 정리하여 나타낸 것이다. 가력 속도가 0.5 mm/s일 경우, 매 사이클별 소산된 에너지량은 평균 8,602 kN·mm으로 나타났다. 이후 가력 속도가 증가함에 따라 하중 증가와 더불어 에너지 소산량도 증가하였으며, 그 증가비율은 하중의 그것과 거의 유사하였다. 가력 속도 1.0 mm/s, 2.0 mm/s, 3.0 mm/s, 5.0 mm/s, 10 mm/s, 15 mm/s, 20 mm/s, 30 mm/s, 그리고 40 mm/s에서 산출된 매 사이클별 평균 에너지 소산량은 각각 9,515 kN·mm, 10,351 kN·mm, 10,963 kN·mm, 11,851 kN·mm, 13,676 kN·mm, 14,610 kN·mm, 15,112 kN·mm, 15,931 kN·mm, 그리고 16,327 kN·mm이었다. 또한, 가력 속도별로 확인한 평균 대비 편차의 최대비율은 대체로 0.5 %에서 2.0 % 사이에 분포하여 감쇠장치 적절성 기준인 15 %보다 훨씬 작은 값을 나타냈다.
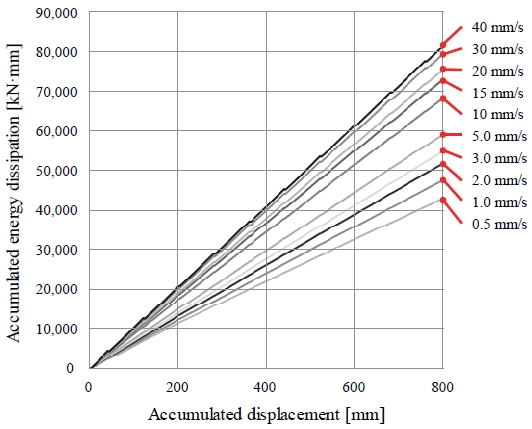
Fig. 6는 누적변위에 따른 누적된 에너지 소산량을 그래프로 나타낸 것이다. 그림에서 확인해 볼 수 있듯이, 댐퍼에 가해지는 변위가 증가할수록 소산되어 누적되는 에너지량이 선형·안정적으로 증가하는 것을 확인해 볼 수 있다. 최저 가력 속도 0.5 mm/s에서 확인된 5회 반복 누적된 에너지 소산량은 약 43,010 kN·mm로 나타났다. 반면, 최고 가력 속도인 40 mm/s에서 확인된 5회 누적 에너지 소산량은 약 81,637 kN·mm로 최저 속도 때 소산량에 비해 약 90 % 가량 더 많은 에너지가 소산된 것으로 확인되었다.
4. 속도-하중 특성 정의
속도의존형 댐퍼의 경우, 제안된 점성 댐퍼를 실제 구조 모델에 적용하여 그 성능을 해석적으로 평가하기 위해서는 댐퍼의 작동 속도에 따른 하중의 크기 변화를 나타내는 함수식 정의가 요구된다. 일반적으로 유체 점성 댐퍼(fluid viscous dampers)의 거동을 나타내는 대표적인 수학 모델로 Maxwell 모델과 Kelvin-Voigt 모델이 주로 사용된다[11]. 본 연구에서는 Maxwell 모델을 적용하여 제안된 댐퍼의 거동을 모사할 수 있는 수치모델을 제안하고자 하였다.
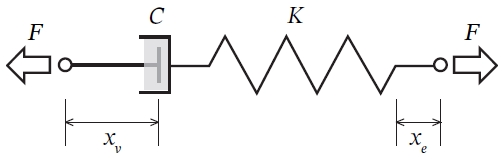
Maxwell 모델은 Fig. 7에서 보이는 바와 같이 스프링 및 감쇠 요소가 직렬로 연결된 형태를 띈다. 이 때문에 전체 시스템에 발생된 변위는 스프링 요소와 감쇠 요소 각각에 발생된 변위의 합으로 나타낼 수 있다(식 (3)). 또한, 각각의 요소에 작용하는 힘은 시스템 전체에 작용하는 힘 F로 식 (4)처럼 정의할 수 있다.
| (3) |
| (4) |
여기서, x, xe, xv는 각각 시스템, 스프링 요소 및 감쇠요소에 발생된 변위를 나타내며, K는 시스템 강성, C는 시스템의 감쇠계수를 나타낸다. 식 (3)에서 각 요소별 변위를 제거하기 위해서 식 (3)과 (4)를 미분하여 재정리하면 식 (5)를 유도할 수 있다.
| (5) |
식 (5)에서 시스템의 강성을 나타내는 K는 본 감쇠장치의 경우 피스톤 로드의 축방향에 대한 강성을 나타내며, 이 값은 감쇠 요소에 의한 저항력보다 매우 큰 값을 나타내기 때문에 두 번째 항은 과 같이 근사할 수 있다. 마지막으로 본 모델에 비선형성을 반영하기 위한 계수 α를 지수로 추가해 주면 식 (6)과 같은 수치모델을 유도할 수 있다.
| (6) |
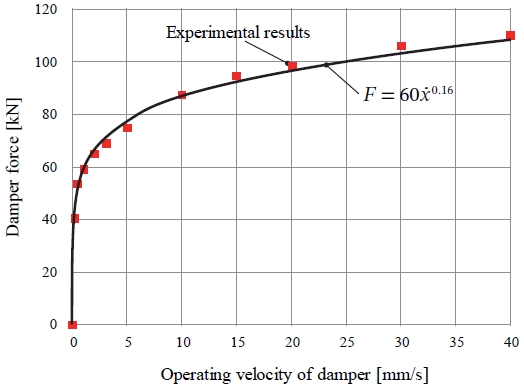
본 연구에서 제안된 댐퍼의 거동을 정확히 예측할 수 있는 함수식을 결정하기 위해서는 상기 방정식에서 적절한 상수값 C와 α가 정의되어야만 한다. 이를 위해 실험으로부터 확인된 제로 변위에서의 평균 하중을 각각의 속도별로 정리하여 Fig. 8에 포인트로 나타냈다. 해당 데이터 분포를 바탕으로 회기 분석을 실시하여, 속도에 따른 하중 증가 경향을 잘 유추할 수 있는 미지 상수값들을 결정하였다. 그 결과 식 (7)과 같이 감쇠계수에 해당하는 C = 60, 비선형성을 나타내는 α = 0.16으로 결정되었으며, Fig. 8에서 보이는 바와 같이 실험 결과와 잘 일치하여 본 댐퍼의 속도-하중 관계를 나타내는 방정식으로 사용하기에 적합함을 확인할 수 있었다.
| (7) |
5. 결 론
본 연구에서는 실리콘 겔이 충전된 점성 댐퍼를 새로 개발 및 제안하였으며, 해당 점성댐퍼의 성능을 다양한 속도 하에서 실험적으로 평가하였다. 그 결과, 다음과 같은 결론을 도출하였다.
- (1) 제안된 실리콘 점성댐퍼는 댐퍼에 발생하는 변위 증가와는 무관하게 하중이 일정하게 유지되었으며, 댐퍼의 작동 속도가 증가할수록 그 저항력은 비선형적으로 증가하는 특성을 나타냈다.
- (2) 성능 평가 실험은 매 가력속도 별로 5회 반복가력을 실시하였으며 그 결과 하중, 유효 강성 및 에너지 소산량에 있어서 평균 대비 편차의 비율이 대부분 2 % 미만으로 계측되었다. 이를 통해 제안된 댐퍼의 감쇠 거동에 대한 신뢰성 및 안정성을 확인할 수 있었다.
- (3) 실험으로부터 확인된 데이터와 Maxwell 모델에 기초하여 제안된 댐퍼의 속도-하중 관계를 정의할 수 있는 함수식을 결정하였으며, 제안된 모델 방정식은 실험 결과와 매우 잘 일치하였다.
Acknowledgments
본 연구는 국토교통과학기술진흥원 국토교통기술촉진연구사업(19CTAP-C142466-02)의 도움을 받아 진행되었습니다.
References
- Ahn, T.-S., and Kim, H.-J. (2008) Efficient Seismic Retrofit of Existing Structures, Review of Architecture and Building Science, Architectural Institute of Korea, Vol.52, No.10, pp.62-69 (in Korean).
-
Shin, H.M., Lee, H.D., and Shin, K.J. (2019) Measurement of Bolt Tension of Friction Damper Using Manufactured Load Cell, Journal of Korean Society of Steel Construction, KSSC, Vol.31, No.3, pp.171-178 (in Korean).
[https://doi.org/10.7781/kjoss.2019.31.3.171]

-
Oh, S.H., Choi, K.Y., and Ryu, H.S. (2012) Structural Performance Evaluations of Steel Hysteretic Damper in Series for High-Rise Shear Wall System, Journal of Korean Society of Steel Construction, KSSC, Vol.24, No.4, pp.371-382 (in Korean).
[https://doi.org/10.7781/kjoss.2012.24.4.371]

-
Lee, D., and Taylor D.P. (2001) Viscous Damper Development and Future Trends, The Structural Design of Tall Buildings, John Wiley & Sons, Vol.10, No.5, pp.311-320.
[https://doi.org/10.1002/tal.188]

-
Pistek, V., Klimes, L., Mauder, T., and Kucera, P. (2017) Optimal Design of Structure in Rheological Models: An Automotive Application to Dampers with High Viscosity silicone fluids, Journal of Vibroengineering, JVE International Ltd., Vol.19, No.6, pp.4459-4470.
[https://doi.org/10.21595/jve.2017.18348]

-
Kim, Y.-G., Cho, K.-H., and Kim, U.-K. (2017) Optimum Design of Propulsion Shafting System Considering Characteristics of a Viscous Damper Applied with High-Viscosity Silicon Oil, Journal of the Korean Society of Marine Engineering, KOSME, Vol.41, No.3, pp.202-208 (in Korean).
[https://doi.org/10.5916/jkosme.2017.41.3.202]

-
Kim, J., Lee, J., and Kang, H. (2016) Seismic Retrofit of Special Truss Moment Frames Using Viscous Dampers, Journal of Constructional Steel Research, Elsevier, Vol.123, pp.53-67.
[https://doi.org/10.1016/j.jcsr.2016.04.027]

- Taylor, D., and Duflot, P. (2002) Fluid Viscous Dampers Used for Seismic Energy Dissipation in Structures, Proceedings of the 12th European Conference on Earthquake Engineering, European Association for Earthquake Engineering, UK.
-
Konstantinidis, D., Makris, N., and Kelly, J.M. (2015) In-Situ Condition Assessment of Seismic Fluid Dampers: Experimental Studies and Challenges, Meccanica, Springer, Vol.50, No.2, pp.323-340.
[https://doi.org/10.1007/s11012-014-9882-4]

- Architectural Institute of Korea (2016) Korean Building Code (KBC 2016) and Commentary, Kimoondang, Korea. (in Korean).
-
Greco, R., and Marano, G.C. (2013) Identification of Parameters of Maxwell and Kelvin-Voigt Generalized Models for Fluid Viscous Dampers, Journal of Vibration and Control, Sage, Vol.21, No.2, pp.260-274.
[https://doi.org/10.1177/1077546313487937]