지관 압축을 받는 고강도강 X형 각형강관접합부의 구조적 성능에 대한 실험적 연구
Copyright ⓒ 2019 by Korean Society of Steel Construction
초록
강관접합부에 고강도강재를 적용하면 많은 구조적 이점을 얻을 수 있다. 그러나 건축구조기준(KBC2016)뿐 아니라 현재 통용되는 국제 구조기준에서도 각형강관 접합부에 고강도강재를 적용하는 것을 금한다. 이러한 제한이 적절한지 확인하기 위하여 본 연구에서는 각형강관 X형 접합부에 대한 실험을 계획하였다. 총 6개의 실험체로 계획된 이 실험은 강종과 지관-주관 폭 비율을 주요 실험변수로 하였다. 지관에 압축력을 가하는 실험을 수행한 결과, 고강도강재로 제작한 실험체에서 발현된 실험강도는 유로코드 3 공칭강도를 상회하였을뿐 아니라 고강도강재에 적용되는 강도감소계수를 적용하지 않은 유로코드 3 공칭강도도 상회하였다. 그중에서 유로코드 3의 주관측벽좌굴 강도는 접합부 강도를 지나치게 저평가하여 개선이 필요하다.
Abstract
The application of high-strength steel to RHS joints can bring many benefits for structures, but it is forbidden or permitted with high-strength penalty in KBC 2016 and most representative international standards. To examine the appropriateness of these limitations, especially the strength reduction penalty imposed on high-strength steels, six RHS X-joint specimens were tested under axial compression. The key parameters of the test are brace to chord width ratios and grades of steels. All high-strength steel specimens exhibited sufficient strength compared to the EC3 strength criteria; their strengths were even higher than the EC3 unreduced nominal strength. It was also found that the formulation of sidewall buckling strength in current EC3 is inaccurate (too conservative) and needs to be improved.
Keywords:
High-strength steel, RHS (rectangular hollow section), X-joint, Cold-formed, Experimental키워드:
고강도강재, 각형강관, X형 접합부, 냉간성형, 실험연구1. 서 론
강관은 구조적 성능을 매우 효율적으로 발휘할 수 있는 단면이다. 특히 기둥이나 트러스 부재로 적용될 때, 폐단면의 특성을 갖는 강관은 압축력 또는 비틀림에 대해 훌륭한 저항성능을 발휘할 수 있다. 강관부재에 고강도강재를 적용한다면 동일 내력을 확보하기 위한 강재량을 획기적으로 줄일 수 있다. 이를 통하여 물량을 줄이고 골조를 경량화하여 시공 시 양중부하를 경감시키는 등 많은 이점을 얻을 수 있다.
국내 현행구조기준 Korean Building Code 2016 (이하 KBC 2016)[1]은 항복강도가 360 MPa을 초과하는 강재를 강관접합부에 적용하지 못하도록 규제한다. Eurocode 3 (EN-1993-1-8, 이하 EC3)[2]는 항복강도가 700 MPa 미만인 강재까지 강관접합부에 적용할 수 있도록 허용한다. 고강도강재 접합부 강도는 일반강재가 적용된 접합부의 강도식을 사용하되, 계산된 값에 강재 항복강도에 따른 강도저감계수(0.8 또는 0.9)를 곱한다. 즉, 본래 계산된 값의 80% 또는 90%만 인정된다.
최근 Lee et al.[3]은 연구를 통해 고강도 원형강관 접합부에 대한 규제로 EC3[2]에서 제시하는 강도감소계수가 적절한지 검토하였다. 이 연구진이 선행연구를 추적한 결과, 강도감소계수를 도입한 공학적 배경과 근거가 미약하다는 결론을 내렸다. 좀 더 면밀한 검증을 위해 접합부의 기하학적 형태와 강종을 변수로 9개 원형강관 접합부 실험체를 계획하여 압축실험을 수행하였다. 추가적으로 이 실험을 뒷받침할 수치해석 모델을 수립하여 실제 압축실험 결과와 비교 · 분석하였다. 그 결과, 고강도강재를 적용한 원형강관 접합부도 일반강재 원형강관 접합부에 준하는 강도와 사용성을 발휘할 수 있음을 확인하였다.
그러므로 본 연구에서는 실험을 통해 고강도강재로 제작된 각형강관 접합부의 강도와 거동을 확인하여 Lee et al.[3]이 고강도 원형강관 접합부에 대해 수행한 연구의 결론을 각형강관 접합부로 확장 · 적용하고자 한다.
2. 선행연구 및 현행기준
1965년 Stewarts and Lloyds[4]의 실험을 시작으로 1960년대부터 1980년대까지 다양한 종류의 강관접합부(X형, T형, K형)에 대해 연구가 이루어졌다. 이 시기에 수행된 실험과 그 결과를 설명하기 위한 이론적 연구를 통해 강관접합부 강도식이 제안되었다(Johansen[5]; Mouty[6]; 그리고 Wardenier[7]). 제안된 강도식들은 IIW (International Institute of Welding) design recommendation[8]과 CIDECT (Committee for International Development and Education on Construction of Tubular structures) design guide 1st Edition (이하 CIDECT 1st Edition)[9]에 반영되었으며, 오늘날 적용되는 구조기준 강도식 대부분이 상기 설계지침들에 기반을 둔다.
2.1 각형강관 접합부의 적용한계
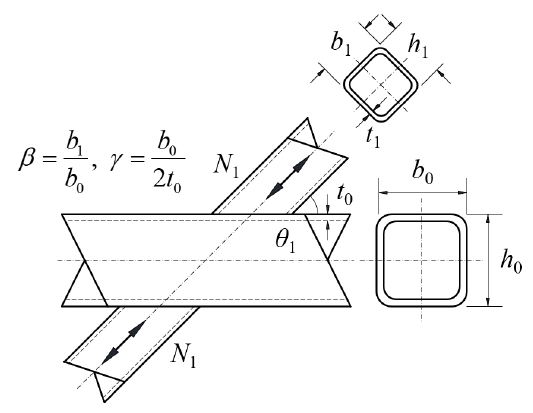
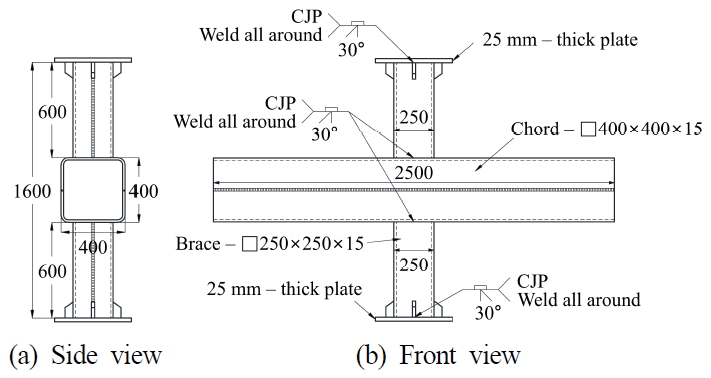
Table 1과 2는 각각 각형강관 접합부의 기하학적 변수들과 재료의 적용한계를 나타낸다. Fig. 1.은 각형강관 X형 접합부의 일반적 형상과 기호를 보여준다. 강관접합부의 주관과 지관 단면은 조밀단면 조건(Class 1 또는 Class 2)을 만족해야 한다.
The AISC(American Institute of Steel Construction) specification 2010 (이하 AISC 2010)[10]은 각형강관 접합부에 항복강도(fy)가 360 MPa을 초과하거나 항복비(YR = fy/fu)가 0.8을 넘는 재료를 사용하지 못하도록 제한한다. 이는 사실상 고강도강재의 적용 자체를 금하는 것이다.
CIDECT design guide 2nd Edition (이하 CIDECT)[11]는 이보다 관대하여 항복강도가 460 MPa를 초과하지 않는 강재까지 각형강관 접합부에 적용될 수 있도록 허용한다. 다만 355 MPa 이상, 460 MPa 미만의 항복강도를 갖는 강재를 각형강관 접합부에 적용하면 계수 0.9를 곱해 공칭강도를 감소시키도록 한다. 또한 항복비가 0.8이 넘는 강재도 허용하지만 이를 적용한 접합부의 강도를 산정할 때에는 사용되는 항복강도를 fy에서 0.8fu로 낮춘다.
EC3[2]는 항복강도가 700 MPa에 달하는 고강도강재까지도 각형강관 접합부에 적용할 수 있도록 허용한다. 그러나 항복강도가 460 MPa 이상, 700 MPa 미만인 강재를 적용할 경우 CIDECT[11]에서 제시하는 강도감소계수 0.9보다 더 작은 0.8을 강도식에 곱해야 한다. 항복강도가 460 MPa 이상인 강재는 항복비 상한이 0.95로 확장된다.
기하학적 변수 β(= b1 / b0)는 지관과 주관의 폭 간 비율을 나타낸다. KBC 2016[1], EC3[2], AISC 2010[10]에서는 0.25이상의 β값을 갖는 접합부만 적용할 수 있게 제시하지만, CIDECT[11]에서는 β값이 0.1+0.01b0/t0보다 커야한다는 조건을 추가로 제시한다. Wardenier[12]의 연구에 따르면 β값은 지관을 통해서 주관으로 외력이 전달되는 메커니즘에 영향을 미친다. 때문에 β는 각형강관과 원형강관 모두에 대해서 강도 및 거동을 결정하는 주요변수이다.
2.2 각형강관 접합부 강도식
원형강관 접합부가 기하학적 적용한계를 만족시키면, 0.20이상 1.00이하 β값을 갖는 접합부에 대해 주관소성화(chord plastification) 또는 펀칭전단 파괴모드(punching shear failure)가 발현된다. 각형강관 접합부가 기하학적 적용한계를 만족하는 경우에는 β값 0.25이상 1.00이하의 범위 내에서 주관소성화와 주관측벽좌굴(chord sidewall buckling), 그리고 두 파괴모드가 혼합된 혼합파괴모드(mixed failure mode)가 나타난다.
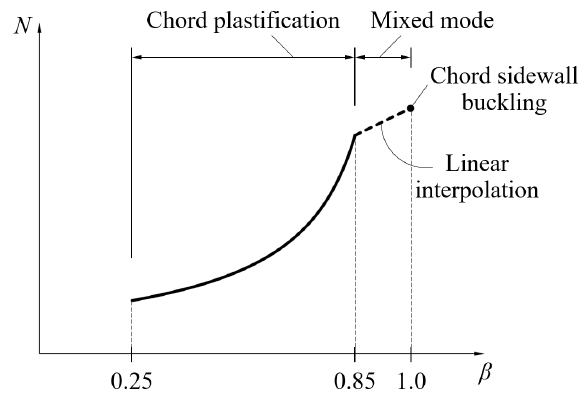
EC3[2]와 CIDECT[10]는 β값에 따라 이 세 파괴모드의 강도 중 한 값을 접합부 강도로 결정하도록 제시한다(Fig. 2.). EC3[2]를 기준으로 할 때, 0.25 ≤ β ≤ 0.85 범위에 속한 상대적으로 작은 β값을 가질 때는 주관소성화 강도를, 주관과 지관의 폭이 동일한 경우(β = 1)에는 주관측벽좌굴 강도를 통해 접합부의 강도를 결정한다. 0.85초과 1미만인 β값의 접합부는 주관측벽좌굴 강도식과 β = 0.85에 대한 주관소성화 강도식을 선형보간하여 강도를 결정한다(Fig. 2. 점선 참조).
한편, AISC 2010[10]에서는 β=1인 접합부 강도를 산정할 때 다른 기준들과는 다르게 웨브국부좌굴(web crippling) 강도식을 사용한다. AISC 2010[10]에서는 0.85 < β < 1.00인 접합부 강도를 별도로 규정하지 않는다. The AISC specification 2016[13]에서도 해당강도를 제시하진 않지만, 웨브국부좌굴 강도식을 사용하길 권한다.
EC3[2]와 AISC 2010[10], CIDECT[11]에서는 0.85 ≤ β < 1.00에 대해 발생 가능한 펀칭전단과 지관국부파단(brace failure)의 강도식도 제시한다. 그러나 두 파괴모드는 적용한계를 만족하는 각형강관 접합부의 일반적인 파괴모드가 아니며, 설계를 통해 배제되어야 한다. 따라서 본 연구에서는 주관소성화와 주관측벽좌굴 강도식에 초점을 맞춰 이론적 모델을 분석하고 실험강도를 평가하는 연구를 진행하였다.
각형강관 X형 접합부의 주관소성화 강도식은 KBC 2016[1], EC3[2], AISC 2010[10], 그리고 CIDECT[11] 에서 식 (1)과 같이 제시된다.
| (1) |
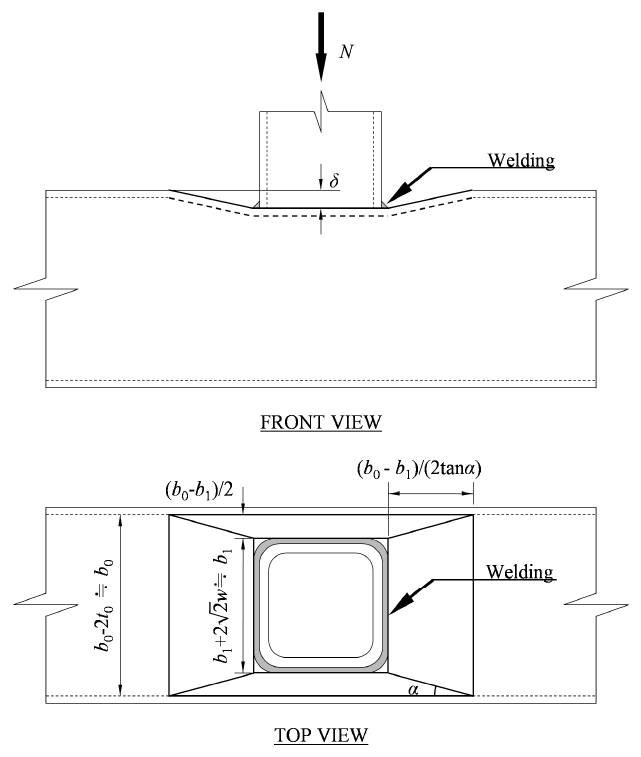
여기서, N1 = 지관에 가해지는 힘, θ1 = 지관과 주관이 이루는 각도, fy0 = 주관단면에 적용된 재료의 항복강도, t0 = 주관단면의 두께, β = 지관과 주관단면의 폭 비율(=b1/b0), h1 = 지관단면의 높이, b0 = 주관단면의 폭, 그리고 Qf = 주관 응력상태에 따라 접합부의 강도를 감소시키는 계수를 나타낸다. 식 (1)에서 Qf를 제외한 항은 rigid perfectly plastic 재료 모델을 적용한 항복선 모델(yield-line model)을 통해 유도된 식이다(Johansen[5], Mouty[6], 그리고 Wardenier[7]). 이 식은 Fig. 3.과 같이 주관 상부면에 항복선이 형성된다고 가정하여 가상일의 법칙(The Work Method)을 적용하여 유도할 수 있다.
주관과 지관 폭이 서로 동일한(β=1) 접합부의 거동은 주관측벽좌굴에 의해 지배된다. EC3[2]와 CIDECT[11]에서 제시하는 주관측벽좌굴 강도식은 식 (2)와 같다.
| (2) |
여기서, χ = 정의된 무차원 세장비 에 따라 얻은 좌굴곡선을 통해 얻는 좌굴강도감소계수이다. χ값을 결정하기 위한 좌굴곡선은 강종과 조관방법에 따라 달라지며, 무차원 세장비 는 아래 식과 같이 정의된다.
| (3) |
여기서, h0 = 주관단면의 높이이며 E = 주관에 적용된 재료의 탄성계수이다.
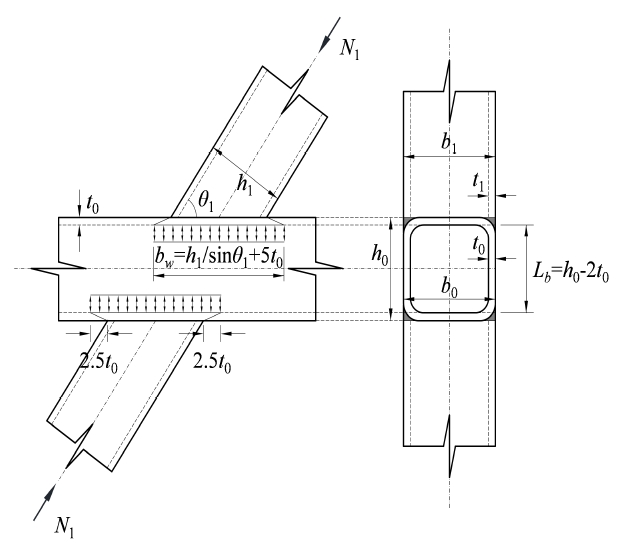
식 (2)는 Wardenier[7]의 연구에서 주관측벽좌굴을 설명하기 위해 제시한 기둥좌굴모델에 기반을 둔다. 해당 모델은 주관측벽의 상단과 하단이 주관 상하부면에 의해 단순지지된다고 가정하고, 주관단면 높이에서 주관단면 두께의 2배를 뺀 h0-2t0를 좌굴길이 Lb로 사용하였다. 또한, 지관에서 주관측벽으로 힘이 전달될 때에 힘을 받는 측벽의 폭 bw가 h1/sinθ1에서 h1/sinθ1+5t0로, 주관단면 두께의 2.5배만큼 좌우측으로 각각 연장된다고 가정한다(Fig. 4. 참조). 이로부터 가정된 기둥의 비탄성좌굴 강도식인 식 (4)를 유도하였다.
| (4) |
이때, 좌굴강도감소계수 χ는 ECCS(European Convention for Constructional Steelwork) recommendation[14]의 기둥곡선 ‘a’, 즉 Rondal-Maquoi equation (Maquoi and Rondal[15])에 불완전계수(imperfection factor) α를 0.206으로 둔 곡선을 통해 결정한다.
식 (2)에 곱해진 계수 0.8은 1/(γmγc)에서 비롯되었다. γm과 γc는 부분안전계수(partial safety factor)로 γm은 재료의 특성을 고려하는 계수며, γc는 해당 구조의 특성과 거동 및 한계상태의 위험성을 고려하는 계수이다. Wardenier는 강구조에 대해서 γm값을 1로 제안하였으며, β가 1인 각형강관 X형 접합부의 낮은 변형능력을 고려하여 γc값으로 1.25를 제안하였다. 최종적으로 식 (4)의 좌변에 곱해진 sinθ1 항을 상쇄하고 우변에 0.8과 Qf를 곱하여 구성된 식 (2)를 IIW 1989[8]와 CIDECT 1st Edition[9]에서 제안하였다.
앞서 언급했듯이 AISC 2010[10]은 β = 1인 각형강관 X형 접합부의 강도를 다른 구조기준들과 다르게 산정한다. AISC 2010[10]은 Chen and Oppenheim[16]의 연구에서 제안된 H형강의 웨브국부좌굴 강도식을 각형강관 접합부에 적용한 식(식 5)과 주관측벽의 항복강도식(식 6) 중 작은 값으로 결정한다. 두 식은 아래와 같다.
| (5) |
| (6) |
여기서 k는 절곡된 주관 단면의 외측 반경이며 1.5t0보다 작지 않은 값을 사용한다.
2.3 강재의 항복강도에 따른 강도저감계수
각 기준에서는 각형강관 접합부에 적용되는 강재의 항복강도와 항복비를 제한한다. 더불어 강재 항복강도에 따른 강도감소계수를 통해 산정된 강도의 80% 또는 90%만 인정한다(Table 2 참조). 이 강도저감계수는 K형 접합부에 대한 연구에서 비롯되었다. Kurobane[17]는 고강도강재가 적용된 CHS gapped K-joint에 대한 실험을 수행하였고, 실험체의 강도를 실험체에 적용된 강재의 항복강도로 나눈 값을 통해 비교하였다. 그 결과, S460(fy = 460 MPa)을 적용한 접합부를 통해 얻은 값이 동일한 형상을 갖는 일반강재(S235) 접합부 실험체를 통해 얻은 값에 비해 20%정도 작았다. 이 연구결과를 토대로 강도감소계수가 처음 제시되었으며, Noordhoek et al.[18]이 수행한 CHS gapped K-joints 실험에 의해 재확인되었다. Mang[19]은 각형강관으로 만든 K형 접합부에 고강도강재(S690)를 적용하여 실험을 수행하였으며, 그와 비교하기 위해 제작된 S235 접합부에 비해 상대적으로 감소된 강도를 확인하였다. 또한 S460로 제작된 RHS gapped K-joint에 대한 수치해석 결과를 통해 Liu and Wardenier[20]는 강도감소계수 0.9가 적용되어야 한다고 주장하였다.
이와 달리 고강도강재가 적용된 X형 접합부에 대한 선행연구들에서는 해당 강도감소계수가 너무 보수적이라는 실험적 근거들이 제시되었다. Puthli et al.[21]은 원형강관 X형 접합부에 대한 실험과 이를 보완하는 수치해석 연구를 수행하였다. 이 연구에서는 실험을 통해 얻은 접합부 강도가 강도감소계수 0.9를 곱하지 않은 공칭강도를 상회하였다고 보고한다. C450으로 제작된 각형강관 T형, X형 접합부에 대한 연구를 수행했던 Becque and Wilkinson[22]도 감소되지 않은 공칭강도 대비 실험강도(Nexp/NCIDECT,unreduced)가 1보다 더 크거나 근소하게 작은 값을 보였으며, 0.9의 강도감소계수가 너무 보수적이라는 주장에 힘을 실었다.
앞에서 언급한 Lee et al.[3]의 연구에서는 항복강도가 460 MPa을 초과하는 고강도강재로 원형강관 X형 접합부 실험체 6개를 제작하여 실험을 수행하였다. 실험결과와 데이터베이스를 확충하는 수치해석을 통해 고강도강재를 적용한 접합부가 강도적, 연성적 측면에서 충분한 성능을 발휘할 수 있다는 결론을 이끌어냈다. 따라서 본 연구에서는 이 결론을 각형강관으로 확장하기 위해 460 MPa을 초과하는 강재가 적용된 각형강관 X형 접합부 실험을 계획하고 접합부 공칭강도 산정 시 도입되는 강도감소계수 0.8이 적합한지 확인하고자 한다.
3. 실험계획
3.1 실험체 계획 및 제작
주요 실험변수는 강종(항복강도로 구분됨)과 지관-주관 폭 비율인 β이다. 본 연구에서는 2개의 서로 다른 강종인 SM490(현 SM355)와 HSA800(현 HSA650)을 사용하였으며, 3개의 β값(0.625, 0.85, 1)을 적용하여 총 6개의 실험체를 계획하였다(Table 3 참조). 실험체는 X형 접합부를 나타내는 “X”와 그에 뒤따라오는 “θ1-fyn-β-2γ”로 명명된다. 모든 실험체는 기하학적 적용한계를 만족시켜 주관소성화와 주관측벽좌굴 이외의 파괴모드를 배제하였다.
지관과 주관은 ㄷ형강 2개를 용접하여 제작하며, 제작과정은 다음과 같다. 프레싱머신(pressing machine)에 강판을 절곡하여 내부반경이 30 mm인 ㄷ형강을 만들고(Fig. 5.) 서로 다른 ㄷ형강의 다리 부분을 맞댔을 때 V형 개선이 형성되도록 가공한다. 이후 형성된 V형 개선에 뒷댐재(backing strip)를 놓고 완전용입용접(complete joint penetration, CJP)하였다. SM490 강재로 제작된 ㄷ형강 채널에는 K71T(KS D 7104[23], YFW-C50DR), HSA800 강재로 제작된 채널에는 PKW900(AWS A5.29-07[24], E121T1-G) 용접봉을 사용하여 매칭용접하였다.
Fig. 6.은 실험체의 대표 도면이다. 실험체의 주관 및 지관의 길이는 각각 2500 mm, 600 mm로, 모든 실험체에 동일하게 적용되었다. 지관의 길이는 지관 단면의 최대 폭인 400 mm의 1.5배로 제작하여 지관에 주어지는 압축력을 균일하게 주관으로 전달할 수 있도록 설계하였다. 주관의 용접선은 용접이 실험강도에 미칠 수 있는 불리한 영향까지 고려하기 위하여 주관측벽의 중앙에 배치하였다. 또한 25 mm 두께의 단부 강판을 설치하여 가력 시 지관 단면에 응력이 고르게 분포할 수 있게 하였으며, 지관 단부에서 취약한 거동이 발생되지 않도록 스티프너로 보강하였다.
3.2 실험 셋업
본 연구에서는 6개 각형강관 접합부 지관에 최대용량 10,000 kN UTM(Universal Testing Machine)으로 압축력을 가하는 정적가력실험이 수행되었다. Fig. 7.은 대표적인 실험 셋업을 보여준다. 모든 실험체가 수평 방향으로 충분히 안정되었다고 판단하여 횡방향으로 지지하지 않고 실험을 수행하였으며, 실험결과, 어떤 실험체에서도 수평방향 좌굴과 같은 불안정성(instability)을 확인할 수 없었다.
주관 상하부면의 면외방향 변형을 계측하기 위하여 6개의 LVDT(linear variable differential transformers)를 Fig. 7.(c)와 같이 실험체에 부착하였다. 그러나 본 실험에서는 주관측벽의 면외방향 변형을 계측하지 못해 β=1 실험체의 좌굴시점을 확인할 수 없었다.
4. 실험결과 및 분석
4.1 인장시험결과
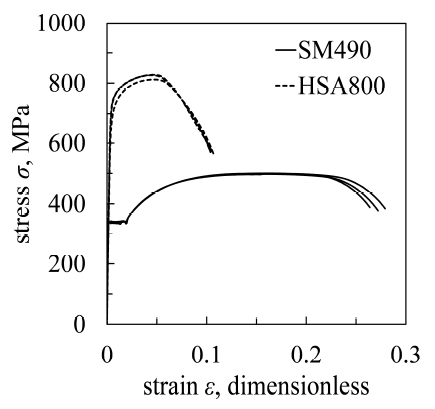
강관제작에 사용될 강판이 아직 냉간성형되기 전에 서로 다른 강종(SM490과 HSA800)의 두 강판에서 각각 3개씩 시편을 채취하였다. Fig. 8.은 확보한 6개 시편에 인장시험을 수행해 얻은 응력-변형률 관계를 일반강재와 고강도강재로 각각 구분하여 나타낸다. SM490 시편의 응력-변형률 곡선은 항복참(yield plateau)과 변형경화현상(strain-hardening)이 분명히 나타나는 전형적인 일반강재의 연성거동을 보였다. 반면 고강도강재(HSA800)는 항복참이 뚜렷하게 나타나지 않았으며, 일반강재보다 상대적으로 작은 변형률에서 극한강도를 발현하였다. 인장시험 결과는 Table 5에 정리하였다. 앞에서 언급하였듯, 본 인장시험에 사용된 시편들은 강관 제작 전에 채취되었기 때문에 냉간성형에 따른 항복강도 증가 효과는 나타나지 않았다.
4.2 접합부 압축실험 결과
β = 0.625인 두 실험체는 계획된 실험체 중에서 가장 우수한 변형능력을 보였다. X90-325-0.625-26.7 실험체는 Fig. 9.와 같이 육안으로 보기에도 확연한 큰 변형을 일으켰으며, 이러한 변형에도 저항력을 잃지 않았다. 해당 실험체의 압축실험은 주관 상하부면이 서로 맞닿기 직전, 면외방향 변형이 주관 폭 b0의 42.8%에 달하였을 때 중단되었다.
X90-650-0.625-26.7 실험체는 HSA800 강재를 적용한 실험체로, X90-325-0.625-26.7 실험체와 기하학적 형상은 동일하지만 변형능력에서 큰 차이를 보였다. X90-650-0.625-26.7 실험체는 주관 폭의 13%만큼 면외변형을 일으켰을 때 주관하부면에 위치한 지관 단면의 꼭지점 부근에서 시작된 파단으로 인해 급격하게 내력을 상실하였다(Fig. 10. 참조).
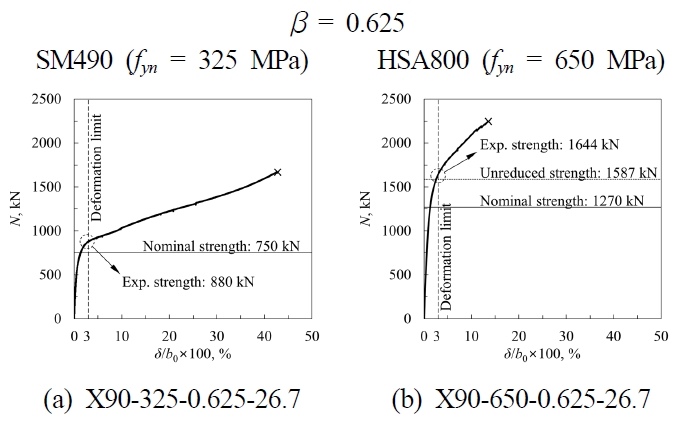
Fig. 11.(a)와 (b)는 β = 0.625인 두 실험체의 하중-변형 곡선을 보여준다. 두 실험체 모두는 주관 상하부면의 변형이 증가함에 따라 지속적으로 접합부의 강도도 증가하는 경향을 나타내기 때문에 Lu et al.[25]의 연구에서 제안한 극한변형한계인 주관폭의 3% 면외변형을 기준으로 강도를 결정하였다(Fig. 11.(a)와 11.(b)에 점선으로 그려진 Deformation limit 참조).
그 결과, SM490을 적용한 실험체의 강도는 880 kN, HSA800을 적용한 실험체의 강도는 1644 kN으로 나타났다. 이는 현행구조기준들에 제시된 주관소성화 강도식을 통해 산정된 강도의 117%, 129%에 달하는 강도다(Table 5). 비록 X90–650–0.625–26.7 실험체가 주관하부면이 파괴되어 내력을 상실했지만, 이 실험체 역시 극한변형한계인 면외변형(3%b0)를 초과하는 변형에 저항할 수 있음을 확인하였다.
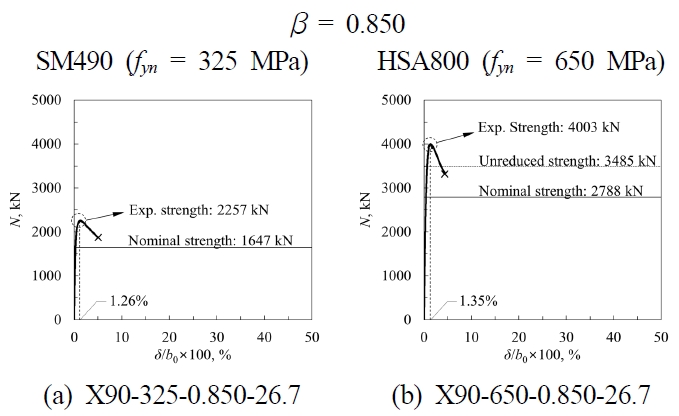
β = 0.850인 두 실험체 모두는 면외변형이 주관 폭의 약 1%에 도달하였을 때 최대하중이 나타난다. 이들은 β = 0.625인 실험체에 비해 훨씬 강성이 크며 취성적인 거동을 보인다. 그러나 내력의 20%를 소실하기 전에 극한변형한계(3%b0)에 도달하여 비교적 양호한 변형능력을 보였다(Fig. 12. 참조). 한편, 두 실험체가 최대하중에 도달할 때의 면외변형은 거의 동일하였다. 이는 강재의 특성으로 인한 접합부 거동의 차이가 거의 없다는 사실을 시사한다.
EC3 공칭강도에 대비한 실험강도는 각각 137%(SM490 실험체), 144%(HSA800 실험체)로 나타났다. 이는 EC3[2]가 접합부의 강도를 보수적으로 평가한다는 사실을 보여준다. 심지어 실험강도는 강도감소계수 0.8이 적용되지 않은 EC3 강도조차도 충분히 상회하였다(15% 초과).
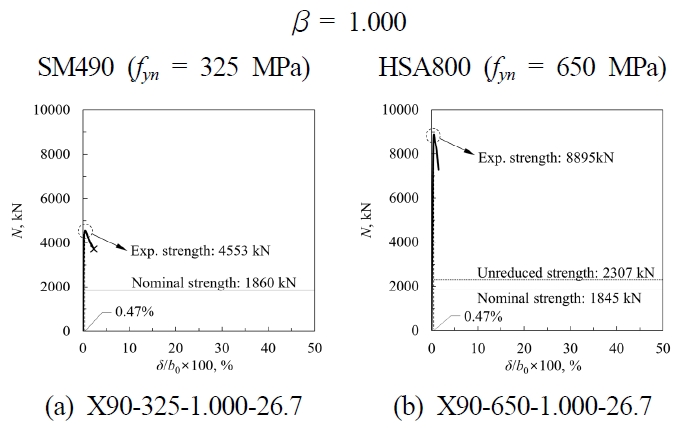
두 β = 1 실험체는 본 연구에서 진행한 실험체들 중 가장 강성이 크고 취성적인 거동을 보였다. 이 두 실험체는 면외변형이 0.47%b0에 달했을 때 최대하중에 도달하며, 극한변형한계(3%b0)에 도달하기 전에 내력의 약 20%이상이 손실되어 실험을 종료하였다(Fig. 13. 참조).
두 실험체의 실험강도를 EC3의 주관측벽좌굴강도로 정규화한 값은 SM490 실험체에 대해 245%, HSA800 실험체에 대해 482%로 나타났다. X90-650-1.000-26.7 접합부의 실험강도는 강도감소계수인 0.8을 곱하지 않은 EC3 강도와 비교하더라도 매우 큰 여유강도를 갖는다(Nexp/NEC3,unreduced = 386%). 이는 EC3의 주관측벽좌굴강도식이 β = 1 접합부의 강도를 매우 저평가할 뿐 아니라 부정확하게 평가하고 있다는 사실을 분명하게 보여준다.
5. 요약 및 결론
본 연구에서 진행한 각형강관 X형 접합부 압축실험의 결과는 다음과 같이 요약할 수 있다.
- 1. 접합부의 거동과 강도가 β값에 따라 크게 변화한다는 사실을 실험을 통해 확인하였다. 이는 β값이 바뀌면 그에 따라 힘의 전달 메커니즘이 달라져 파괴에 이르는 거동 또한 달라지기 때문이다.
- 2. 항복강도가 700 MPa에 달하는 고강도강재를 적용한 모든 접합부 실험체에서 강도감소계수 0.8을 적용하지 않은 EC3 공칭강도를 상회하는 실험강도가 발현되는 것을 확인하였다. 즉, 현행 EC3에서 제안하는 강도감소계수는 너무 보수적이며 그 유효성이 재평가되어야 한다. 따라서 추가적인 실험과 수치해석을 통해 강도감소계수의 유효성을 재고하고, 이 결과를 바탕으로 강도감소계수를 제하거나 수정하여 전 강종을 아우르는 일반적인 설계식을 제안하고자 한다.
- 3. 특히 β = 1인 접합부 실험체의 강도를 산정하는 식인 주관측벽좌굴 강도식은 실험체의 강종과 무관하게 매우 보수적이고 부정확하게 강도를 평가하고 있으며, 그 부정확성은 고강도강재를 적용한 실험체에 대해 상대적으로 더 크게 나타났다. 따라서 보완을 통해 강도식의 정확도를 향상할 필요가 있다.
Acknowledgments
본 연구는 포스코 전문연구교수 사업의 지원을 받아 수행되었습니다. 이에 감사드립니다.
References
-
한국건축학회(2016) 건축구조기준 및 해설. 기문당.
Architectural Institute of Korea (2016) Korean Building Code and Commentary, Kimoondang, Korea (in Korean). - European Committee for Standardization (2005) Eurocode 3: Design of Steel Structures, Part 1.8: Design of Joints (EN-1993-1-8: 2005), Belgium.
-
Lee, C.-H., Kim, S.-H., Chung, D.-H., Kim, D.-K., and Kim, J.-W. (2017) Experimental and Numerical Study of Cold-Formed High-Strength Steel CHS X-Joints, Journal of Structural Engineering, American Society of Civil Engineers, Vol.143, No.8, 04017077.
[https://doi.org/10.1061/(ASCE)ST.1943-541X.0001806]

- Stewarts & Lloyds, Ltd. (1965) The Local Crushing of RHS Conjunctions, Report No. C/E.64/65.1, Stewarts & Lloyds, Ltd., UK.
- Johansen, K.W. (1962) Yield-Line Theory, Cement and Concrete Association, UK.
- Mouty, J. (1978) Behaviour of Welded Joints of Square and Rectangular Tubular Structures: A Theoretical Approach Based on the Method of Yield Lines, IIW Doc. XV-426-78, International Institute of Welding, France.
- Wardenier, J. (1982) Hollow Section Joints, Delft University Press, Netherlands.
- International Institute of Welding (1989) Sub-Commission XV-E: Design Recommendations for Hollow Section Joints – Predominantly Statically Loaded (IIW Doc. XV-701-89, 2nd Ed.), IIW Annual Assembly, Finland.
- Packer, J.A., Wardenier, J., Kurobane, Y., Dutta, D., and Yeomans, N. (1992) Design Guide for Rectangular Hollow Section (RHS) Joints Under Predominantly Static Loading, Verlag TÜV Rheinland, Germany.
- American Institute of Steel Construction (2010) Specification for Structural Steel Buildings (ANSI/AISC 360-10), USA.
- Packer, J.A., Wardenier, J., Zhao, X.-L., van Der Vegte, G.J., and Kurobane, Y. (2009) Design Guide for Rectangular Hollow Section (RHS) Joints Under Predominantly Loading, Comité International pour l'étude et le Développement de la Construction Tubulaire, Netherlands.
- Wardenier, J., Packer, J.A., Zhao, X.-L., and van der Vegte, G.J. (2010) Hollow Sections in Structural Applications (2nd Ed.), Comité International pour le Développement et l´Etude de la Construction Tubulaire, Geneva.
- American Institute of Seel Construction (2016) Specification for Structural Steel Buildings (ANSI/AISC 360-16), USA.
- European Convention for Constructional Steelwork (ECCS) Recommendation.
- Maquoi, R., and Rondal, J. (1978) Mise en Equation des Nouvelles Courbes Européennes de Flambement, Construction Métallique, Vol.1, pp.17-30 (in French).
- Chen, W.F., and Oppenheim, I.J. (1970) Web Buckling Strength of Beam-to-Column Connections, Fritz Engineering Laboratory Report No. 330-10, Fritz Engineering Laboratory (Lehigh University), USA.
- Kurobane, Y. (1981) New Developments and Practices in Tubular Joint Design, Memoirs of the Faculty of Engineering, Kumamoto University, Kumamoto University, Vol.26, No.1, pp.1-57.
- Noordhoek, C., Verheul, A., Foeken, R.J., Bolt, H.M., and Wicks, P.J. (1996) Static Strength of High Strength Steel Tubular Joints (ECSC Agreement Number 7210-MC. 602), European Coal and Steel Community, Luxembourg.
- Mang, F. (1978) Untersuchungen an Verbindungen von geschlossenen und offenen Profilen aus hochfesten Stählen, The Final Report, AIF-Nr. 3347, Karlsruhe University, Germany (in German).
- Liu, D.K., and Wardenier, J. (2004) Effect of the Yield Strength on the Static Strength of Uniplanar K-Joints in RHS, IIW Doc. XVE-04-293, Delft University, Netherlands.
- Puthli, R., Bucak, O., Herion, S., Fleischer, O., Fischl, A., and Josat, O. (2010) Adaptation and Extension of the Valid Design Formulae for Joints Made of High-Strength Steels up to S690 for Cold-Formed and Hot-Rolled Sections, CIDECT Report 5BT-7/10, CIDECT, Germany.
-
Becque, J., and Wilkinson, T. (2012) Experimental Investigation of the Static Capacity of Grade C450 RHS T and X Truss Joints, Proceedings of the 14th International Symposium on Tubular Structures, CRC Press, UK, pp.177-184.
[https://doi.org/10.1201/b13139-27]

-
국가기술표준원(2012) 연강, 고장력강 및 저온용 강용 아크용접플럭스코어선 (KS D 7104: 2012).
Korean Agency for Technology and Standards (2012) Flux Cored Wires for Gas Shielded and Self-Shielded Metal Arc Welding of Mild Steel, High Strength Steel and Low Temperature Service Steel (KS D 7104: 2012), Korea (in Korean). - American Welding Society (2010) Specification for Low-Alloy Steel Electrodes for Flux Core Arc Welding (ANSI/AWS A5.29/A5.29M: 2010), USA.
- Lu, L.H, De Winkel, G.D, Yu, Y., and Wardenier, J. (1994) Deformation Limit for the Ultimate Strength of Hollow Section Joints. Proceedings of the 6th International Symposium on Tubular Structures, IIW, Australia, pp.341-347.