단일보강재로 보강된 하이브리드 보강강판의 면내 압축강도


Copyright © 2019 by Korean Society of Steel Construction
초록
일반교량용 강재 SM355와 고성능강재로 개발된 HSB460 및 HSB690으로 혼합구성되고 단일보강재가 설치된 하이브리드 강판의 극한 면내 압축강도에 대한 면밀한 검토가 수행되었다. 단일보강재의 휨강성과 세장비가 강도에 미치는 영향을 비선형 유한요소해석을 통해 분석하였고 설계기준과 비교검토하였다. 판과 보강재사이 하이브리드 상호작용은 경미하였고 보강판 시스템의 압축강도는 판의 항복강도와 보강재의 폭-두께비에 의해 결정되는 경향을 보였다.
Abstract
Ultimate in-plane compressive strengths have been scrutinized for the hybrid stiffened plate with single stiffener fabricated with SM355 steel that is a conventional steel widely used for general bridges and with HSB460 and HSB690 steels that have been developed for high performance steels. Effects of flexural rigidity and slenderness ratio of single stiffener was investigated on the compressive strengths by nonlinear finite element analysis and compared with design codes. It has been found that hybrid interaction between plate and stiffener is not significant on the compressive strengths that are mainly dependent on the plate yield strength and the width-to-thickness ratio of the stiffener.
Keywords:
in-plane compressive strength, hybrid stiffened plate, single stiffener, high performance steel, finite element analysis.키워드:
면내압축강도, 하이브리드 보강판, 단일보강재, 고성능강, 유한요소해석1. 서 론
최근 초장대교량 및 초대형 구조물의 시공 시 구조물의 경량화 및 유지관리 비용 절감과 생산성이 좋은 고성능강재(high performance steel)가 도입되고 있는 추세다. 교량용 고강도강재로 개발된 HSB (high performance steel for bridge) 강재는 기존 일반 강재 대비 강도, 인성, 용접성, 시공성 등이 향상되어 강교량 건설에 많이 활용되고 있다. 교량구조물에서 압축 판부재에 적용되는 보강판 시스템에서 보강되는 판과 보강재의 강종을 달리하여 제작한 하이브리드 보강판 시스템(hybrid stiffened plate system)을 적용하면 기존의 균질한 보강판 시스템보다 경제성 및 형고저감의 효과를 기대볼 수 있다.
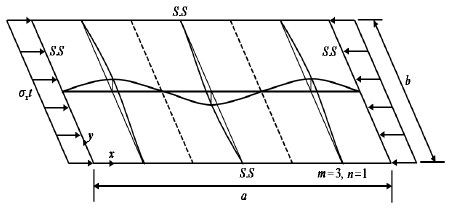
면내력을 받는 보강판의 탄성좌굴모드(elastic buckling mode)는 보강재의 강성에 따라 Fig. 1.에 보인 바와 같이 대칭모드(symmetric mode) 및 역대칭모드(antisymmetric mode)로 구분된다. 보강재 자체의 휨강성이 부족할 경우 보강재가 판과 함께 휘는 현상인 대칭모드를 보이게 되고, 보강재 휨강성이 일정이상 확보될 경우 Fig. 1.(b)역대칭모드를 보이면서 보강판의 면내 압축강도는 효율적으로 향상된다. 여기서, 보강재와 판이 만나서 이루는 접선이 Fig. l.(a)의 경우와는 달리 직선을 유지하여 그 선상에서 면외 변형(out-of-plane deformation)을 방지하고 있음을 알 수 있는데 이 때 이 직선을 절선(nodal line)으로 정의하고, 이 절선의 형성을 보강판 시스템의 탄성해석에서 보강재 강성이 만족 여부에 대한 판단기준이 된다[1].
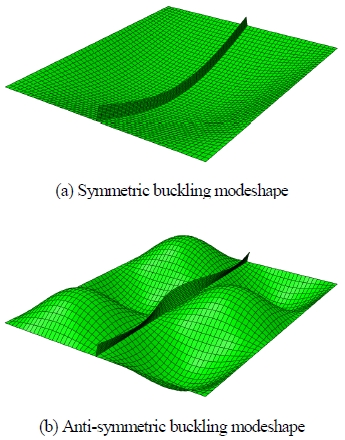
Buckling modeshapes of stiffened plate with single longitudinal stiffener in simply-supported boundary condition
보강재와 판이 만나서 이루는 접선, 즉 보강재가 설치되는 라인이 Fig. 1.(b)에 보인 바와 같이 절선(nodal line)으로 기능하는 탄성좌굴을 유도하기 위한 보강재의 최소강성은 T형 보강재를 대상으로 Yoo et al.[2]이 제안하었다. 판형에 대해서는 Thang et al.[3]이 해석적 연구를 통해 제안하였으나 보강재의 국부좌굴거동이 해석에 고려되지 않았다. 보강재의 휨강성(flexural rigidity)은 보강되는 판의 두께 중심선을 기준으로 한 단면2차모멘트를 기준으로 하지만 판형 보강재의 경우 세장비가 커지면 보강재 자체의 국부좌굴여부가 추가로 검토되어야 한다.
본 연구에서는 우선 교량구조물에 널리 이용되는 SM355 강재를 기본으로 하나의 판형 보강재(single flat-type stiffener)로 보강된 보강판 시스템을 대상으로 탄성해석을 실시하고 좌굴강도를 평가한다. 그리고 비선형 증분해석(nonlinear incremental analysis)을 수행하여 잔류응력과 초기결함에 따른 비탄성거동을 분석한다. 보강재의 폭-두께비(width-to-thickness ratio)로 정의되는 세장비(slenderness ratio)와 휨강성(flexural ridity)을 변수로 극한강도해석을 수행하여 효과적인 보강재의 강성 요구조건을 검토하고, 단면비 제한에 대한 기존의 설계 기준과 비교·검토한다. 해석방법으로 범용 구조해석 프로그램인 ABAQUS[4]를 이용한다. 나아가 SM355 강재와 더불어 HSB460, HSB690 강재를 추가하여 판과 보강재의 강종을 다르게 적용한 하이브리드 보강판 시스템 구조를 채택하여 판과 보강재의 강종 조합에 따른 면내극한강도를 비교·분석한다.
2. 판좌굴강도 이론적 배경
균질하고 Hooke의 법칙을 따르는 탄성 재료 영역에서 압축력을 받는 판의 면내 탄성좌굴강도 유도는 Timoshenco and Gere[5]와 Szilard[6] 등의 문헌에서 참조가 가능하다. 변형률-변위 관계, 응력-변형률 관계, 모멘트-응력 관계, 전단력-응력 관계, 축력-응력 관계 등을 단계적으로 고려하면 판의 지배방정식은 판의 처짐량 w에 대하여 다음과 같이 4차의 비제차 편미분방정식(nonhomogeneous biharmonic equation)으로 표현된다.
| (1) |
여기서, q는 판에 수직으로 작용하는 하중이고, D는 판의 휨강성(flexural rigidity)으로 다음과 같이 정의된다.
| (2) |
식 (1)의 지배편미분 방정식의 가능한 해의 하나로 Levy type의 해[6]를 가정하고, 4변에 대한 단순지지조건으로 해를 정리하면 다음과 같다.
| (3) |
여기서, k는 좌굴계수로서 Fig. 2.에 보인 판의 형상비(aspect ratio, α = a/b)와 축방향 사인 반파장(half sine wave length)의 수 m으로 표현된다.
| (4) |
여기서, m = 1, 2, 3, …
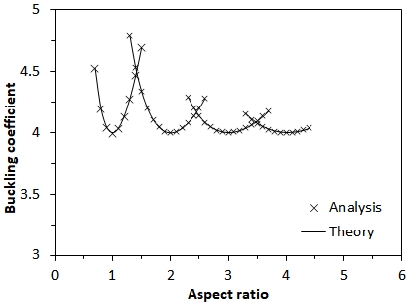
판의 형상비가 주어지면, 식 (4)의 미분, 즉 dk/dm = 0으로부터 m에 따른 최소좌굴계수 kmin를 구할 수 있다. 식 (4)로부터 판이 단순지지된 경우 kmin = 4가 됨을 알 수 있다. 단순 지지된 판이 면내 하중(in-plane force)을 받을 때 탄성좌굴강도가 식 (4)로 유도된 탄성좌굴강도의 좌굴계수와 얼마나 잘 부합하는지 확인을 위해 유한요소해석 프로그램 ABAQUS[4]의 고유치 해석을 수행하였다. 예제에 사용된 판의 치수와 재료상수는 Table 1에 나타내었다. 형상비 α = a/b와 축방향 반파장의 수, m를 변화시키며 해석으로 구한 좌굴계수를 식 (4)의 이론값과 함께 Fig. 3.에 도시하였다. Fig. 3.에서 확인할 수 있듯이 탄성좌굴의 경우 수치해석적 방법에 근거한 유한요소해석과 해석적 방법론으로 유도된 좌굴계수는 매우 잘 일치함을 알 수 있다.
3. 보강판 강도 설계기준
건설기준 코드체계 전환에 따라 통합 정비된 KDS 24 14 31 강교설계기준(한계상태설계법)[7]에서는 면내 압축력을 받는 보강판으로서 박스거더 플랜지 강도 산정방식을 제시하고 있는데, 그 상세는 KDS 14 31 10 강구조부재설계기준(한계상태설계법)[8]을 따르도록 규정하고 있다. 해당 설계기준을 살펴보면 압축플랜지의 공칭강도 Fnc는 응력 단위로 다음과 같이 제시하고 있다.
| (5) |
여기서, Fcv는 전단만 작용할 때 플랜지의 공칭전단좌굴강도를 나타내고, 플랜지의 공칭압축좌굴강도에 해당하는 Fcb는 다음과 같이 구한다.
① λf ≤ λp인 경우:
| (6a) |
② λp < λf ≤ λr인 경우:
| (6b) |
③ λf > λr인 경우:
| (6c) |
여기서,
(압축플랜지의 세장비)
Fyr = (Δ - 0.3)Fyc ≤ Fyw
fv : 계수하중에 의한 플랜지의 순수비틀림 전단응력
Rb : 웨브 응력감소계수
Rh : 하이브리드 단면 응력감소계수
균일분포 압축응력에 대한 판의 좌굴계수 k는 판의 보강재 유무에 따라 다르게 계산된다. 보강재가 없는 경우에는 단순지지조건으로 구한 k = 4.0로 치환될 수 있지만 보강재가 설치된 경우에는 다음과 같은 과정으로 구한다.
우선 플랜지 폭 bfc는 압축플랜지의 종방향보강재 사이 폭 또는 웨브로부터 가장 가까운 종방향보강재까지의 거리 중 큰 값 w로 대체한다. 등분포 수직응력에 대한 판 좌굴계수 k는 보강재의 개수 n에 따라 아래와 같이 구한다.
| (7a) |
| (7b) |
여기서, 1.0≤k≤4.0의 전제조건을 가지며 Is는 플랜지와 평행한 축에 대한 보강재 하단에서의 종방향보강재 1개의 단면2차모멘트, n은 등간격인 종방향보강재의 수, w는 압축플랜지의 종방향보강재 사이 폭 또는 웨브로부터 가장 가까운 종방향보강재까지의 거리 중 큰 값을 의미한다.
기존 도로교설계기준에서 보강재의 개수가 5개까지 적용이 가능하지만 강교설계의 새로운 기준인 강구조부재설계기준 KDS 14 31 10[8]에서는 보강재의 개수는 2개까지만 허용된다. 보강재의 수가 증가될 경우, 필요한 k값을 만족하기 위해 식 (7b)로부터 소요되는 관성모멘트가 극단적으로 증가하기 시작해서 결국 비현실적인 값을 초래하게 되기 때문이다. 따라서, 일반적인 비율의 박스 단면 거더에서 플랜지 종방향보강재의 수는 경제성을 최대화하기 위해서 하나를 초과하지 않도록 하는 것이 적극 권장되고, 최대 2개까지만 고려하는 것이 본 설계기준의 기념으로 이해될 수 있다. 이 경우 각 보강재의 최소 강성으로 단면2차모멘트가 다음 식을 만족하도록 규정되었다.
| (8) |
여기서, ψ는 보강재의 개수 n에 의해 다음과 같이 규정된다.
| (9a) |
| (9b) |
또한 보강재의 국부좌굴을 방지하기 위하여 돌출폭 h는 다음을 만족하여야 한다.
| (10) |
여기서, ts는 수평보강재의 두께, Fys는 수평보강재의 최소항복강도이다.
Yoo et al.[2]은 역대칭 좌굴모드를 구현하기 위해서 보강재가 가져야 할 최소 강성으로 단면2차모멘트의 크기를 다음 식을 제안하였다.
| (11) |
여기서, α는 보강재 사이 서브패널의 형상비(aspect ratio)이다. 식 (11)은 T형 단면을 가지는 보강재를 대상으로 그 개수는 3개 까지 적용하여 유도되었다. Thang et al.[3]은 판형(flat type) 보강재를 대상으로 보강재의 개수에 따라 5개까지 다음 식을 제안하였다.
| (12a) |
| (12b) |
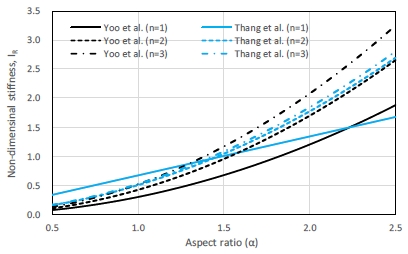
Fig. 4.는 형상비가 0.5 ~ 2.5에 분포할 때 Yoo et al.[2]과 Thang et al.[3]의 연구에서 각각 제안된 보강재 요구강성을 wt3에 대하여 정규화하여 무차원화된 값으로 보였다. 보강재가 하나인 경우 판형(flat type) 보강재 강성이 T형 보강재보다는 요구강성이 다소 높다는 것을 확인할 수 있다. 이는 판형 보강재가 T형보강재보다 국부좌굴에 더 취약하기 때문으로 이해된다.
4. 보강재 국부좌굴 거동
본 장에서는 판형 보강재(flat-type stiffener)의 세장비 및 단면2차모멘트로 표현되는 휨강성이 보강판 시스템의 극한 강도에 미치는 영향을 해석적 기법으로 살펴 본다. 해석 방법은 유한요소해석에 근거한 범용 구조해석 프로그램인 ABAQUS[4]를 이용하여 고유치 해석(eigenvalue analysis)으로 우선 탄성좌굴강도를 확인한다. 또한 ABAQUS에서 제공되는 Modified Riks Algorithm에 근거하여 비선형/비탄성 좌굴강도 해석을 통해 보강판의 극한강도를 확인한다. 고강도강재와 일반강재의 조합으로 구성되는 하이브리드 보강판의 강도평가에 앞서 일반 강재인 SM355을 적용한 균질 보강판 해석을 통해 보강재의 국부좌굴거동 및 요구강성을 검토한다.
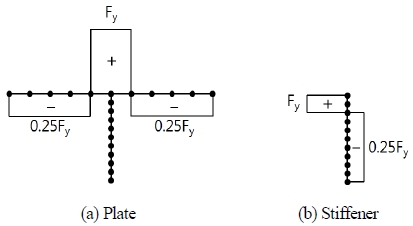
잔류응력(residual stress)은 재료가 외력이나 온도변화를 받고 있지 않아도 그 재료 내에 남아있는 응력으로, 보강판 시스템에서 비탄성 좌굴응력 및 극한 거동에 큰 영향을 주는 요소이다.[9, 10] 보강판 시스템에서도 보강재와 판의 접합부는 용접연결로 가정했기 때문에 잔류응력의 형상을 Fig. 5.에 보인 바와 같이 적용하였는데 용접선 주위에서의 잔류응력을 평형상태로 고려한 것이다.
또한 제작 및 운반 등 완정하지 못한 환경에 의해 발생하는 초기결함(initial imperfection) 또한 강도를 감소시키는 요인이며, 압축부재의 설계에 있어서 반드시 고려해야 한다. 본 연구에서는 초기결함의 모드형상으로 탄성좌굴해석을 통해 얻어진 Fig. 1.에 보인 대칭 좌굴모드(symmetric buckling mode) 및 역대칭 좌굴모드(antisymmetric buckling mode) 두 가지를 기하학적 초기결함의 형상으로 각각 적용하여 극한강도해석을 수행하여 그 중 낮은 강도를 최종강도로 결정하였다. 초기결함의 크기는 보강재와 판의 연단사이 거리 w의 1/100을 적용했다.
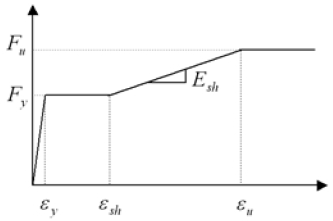
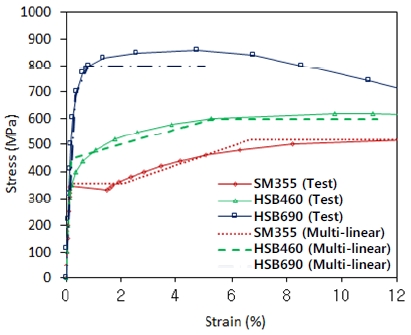
예제에 사용된 강재는 교량용으로 많이 사용되는 SM355 수준의 강재를 적용했다. 사용된 강재의 재료특성은 Fig. 6.에 보인 바와 같이 다중선분(multi-linear) 응력-변형률 관계[11]로 단순화하였으며 해당 값은 Table 2에 나타내었다.
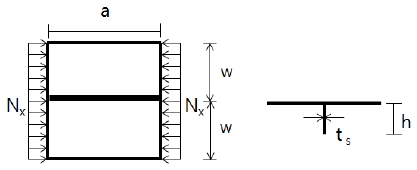
보강판의 경계조건은 Fig. 7.에 보인 바와 같이 4변이 단순지지된 판(simply supported plate)으로 설정하였고, 하중 조건은 단위길이 당 하중으로 보강재의 수평방향으로 재하하였다. 예제에 사용된 보강판의 기하학적 수치 및 재료상수는 Table 3에 제시하였다. Table 3에 보였듯이, 판의 치수는 일정하게 두고 보강재의 높이를 177.8 ~ 330.2 mm의 범위에서, 두께는 10.2 ~ 25.4 mm의 범위에서 변화시켜면서 해석을 진행하였다. 이는 보강재의 휨강성과 더불어 폭-두께비로 정의되는 세장비(slenderness ratio)에 따른 국부좌굴 거동을 살펴보기 위함이다.
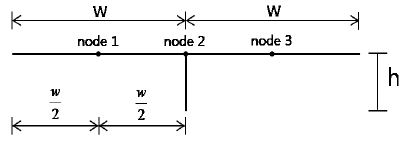
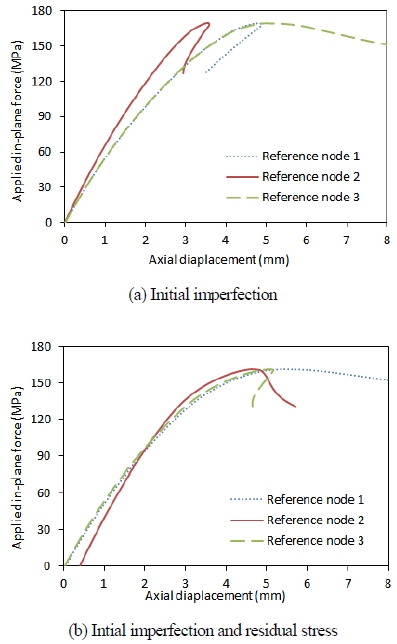
초기결함과 잔류응력의 영향에 의한 보강판의 극한강도 차이를 확인하기 위해 초기결함만 적용한 경우와 초기결함과 잔류응력이 모두 적용된 경우로 나누어 해석하였다. 보강재 두께 25.4 mm 및 높이 241.3 mm를 가지는 모델의 극한강도해석 결과에서 Fig. 8.에 보인 각 참조절점(reference node)에서 면내압축하중에 따른 하중재하방향 변위 관계를 관측하여 Fig. 9.(a) 및 9.(b)에 각각 보였다.
Fig. 9.(a)는 초기결함만이 적용된 경우이기 때문에 세 절점에서 변위 시작점이 같은 것을 알 수 있다. Fig. 9.(b)는 초기결함과 잔류응력이 모두 적용된 경우로서, 잔류응력의 영향으로 보강재 설치 지점인 node 2에서 하중재하 전에 부분적으로 변위가 발생되었음을 확인할 수 있다.
단면2차모멘트로 대표되는 휨강성(flexural regidity)을 영향을 고려하기 위하여 보강재 두께와 판 두께의 비(ts/tf)를 0.4 ~ 1.0까지 0.2씩 증가시켜서 해석을 수행하였다. Table 3에 보였듯이, 이러한 범위에서 판형 보강재단면의 단면2차모멘트는 보강되는 판의 중심선 기준으로 1.9E+7 ~ 3.0E+8 mm4의 값을 가지게 된다.
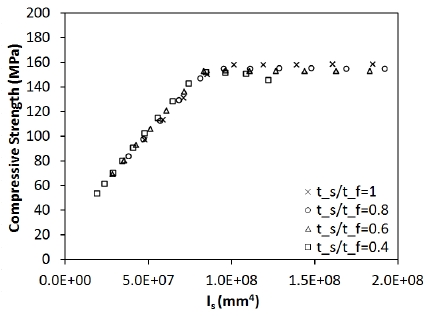
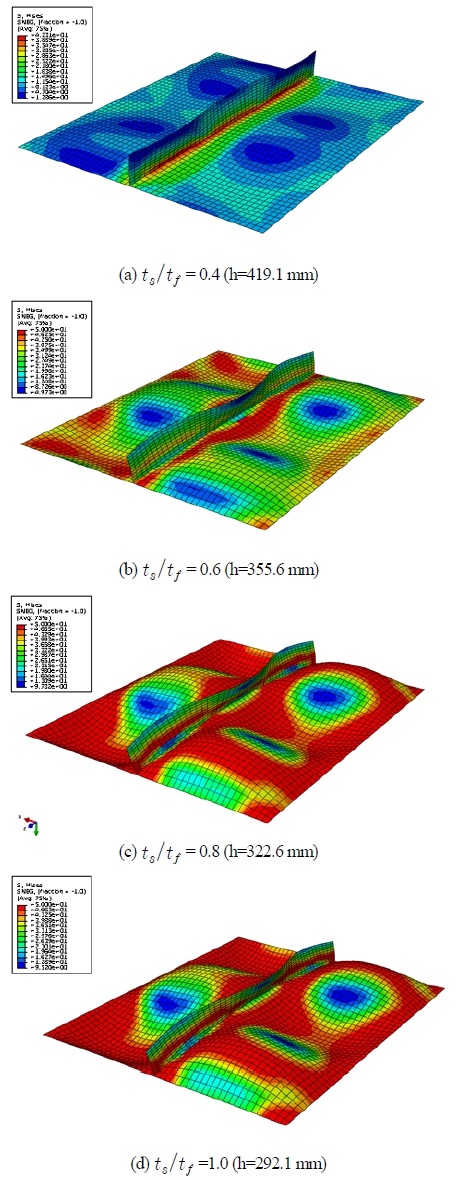
보강재 사이즈에 따른 탄성해석의 결과를 Fig. 10.에 보였다. Fig. 8.에서 확인할 수 있듯이 보강재의 단면2차모멘트가 7.4E+7 mm4수준에 이르면 보강재의 세장비에 상관없이 보강판에 대한 일정 수준의 압축강도는 확보됨을 알 수 있다. 즉, 이 수준의 휨강성이 절선(nodal line)을 형성하기 위한 최소 휨강성으로 이해될 수 있다. 보강재의 강성이 충분하여 절선(nodal line)이 형성되는 역대칭 좌굴모드로 나타나면 좌굴강도는 보강재의 강성이 증가해도 거의 변함이 없는 것을 알 수 있다. 보강재의 세장비에 상관없이 휨강성에만 의존하는 이러한 경향은 보강재의 국부좌굴여부를 제대로 확인하기 어렵다는 것을 의미한다. 초기결함과 잔류응력을 포함하여 재료의 항복이 고려되는 비탄성 극한강도해석의 결과는 Fig. 11.에 보였다. Fig. 11.에서 확인할 수 있듯이 보강재의 세장비가 보강판의 강도에 민감하게 영향을 준다는 사실을 확인할 수 있다. 판에 대한 보강재의 두께비(ts/tf)가 작아 세장한 단면을 가지면 휨강성이 확보된다 하더라도 절선(nodal line) 형성 전에 보강재 자체에 국부좌굴이 발생하기 때문이다[12]. 두께비(ts/tf)가 0.4인 경우는 보강재가 세장하여 보강판 시스템 전체의 극한강도를 보강재의 폭-두께비가 지배하게 된다. Fig. 12.에 휨강성이 비슷한 범위에 있는 대표 모델을 대상으로 극한강도에 도달했을 때 von Mises의 응력분포 및 변형형상(deformed shape)을 보였다.
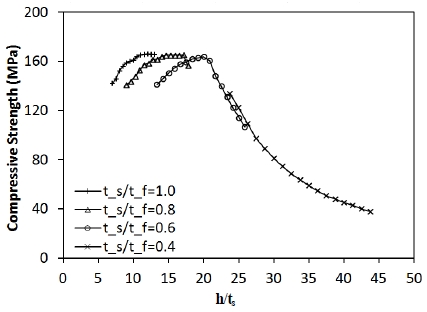
Fig. 13.은 보강재의 세장비(h/ts) 변화에 따른 보강판의 극한압축강도의 분포를 보여준다. 세장비가 20 이하의 범위에서 휨강성이 증가하면 압축강도는 향상된다는 것을 확인할 수 있다. 식 (10)에서 적용 강재의 항복강도 355 MPa과 탄성계수 205 GPa을 대입하면 보인 돌출폭과 두께비 제한은 11.5가 됨을 알 수 있다. 해석에 의한 값 20과 비교해 보면 상당히 보수적인 값으로 제한하고 있음을 알 수 있다.
5. 하이브리드 고강도 강재 보강판
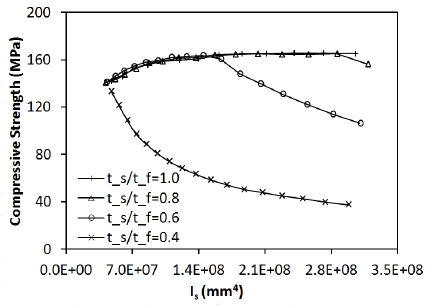
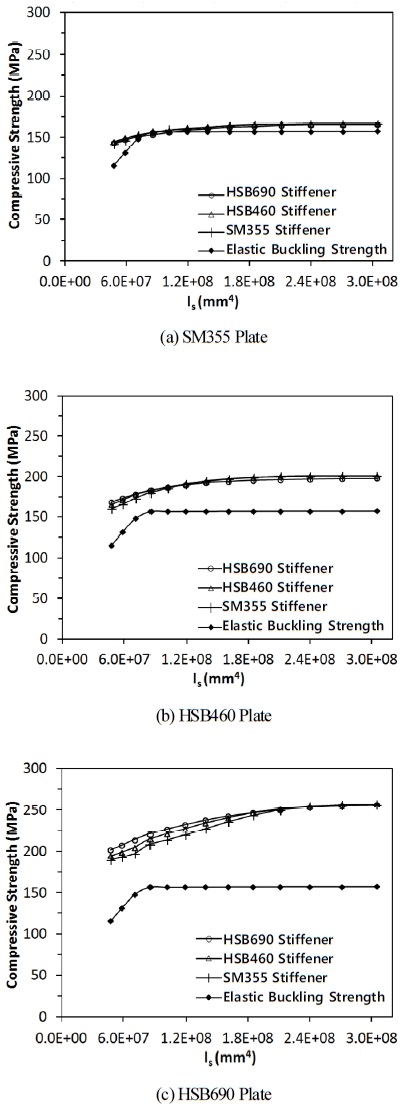
본 절에서는 교량용 고성능 강재인 HSB(high performance steel for bridges) 중에서 HSB460 및 HSB690 강재를 SM355 강재와 조합한 하이브리드 보강판을 형성하여 그 극한강도를 평가한다. 하이브리드 보강판이란 판과 보강재가 서로 다른 강종으로 구성되는 경우를 일컫는다. 또는 고강도강재를 적용한 보강판과 보강재의 두께비에 따른 극한강도를 확인한다. 고성능강재 HSB의 표기에 포함된 460 및 690은 최소한으로 확보되는 항복강도를 의미하는데, 각 각종에 대해 적용된 응력-변형 곡선은 Shin et al.[9],[10]의 연구를 참조하여 Fig. 14.에 보인 바와 같이 다선형(multi- linear)로 가정하여 해석에 적용하였다. 자세한 재료상수는 Shin et al.[9],[10]에서 확인이 가능하다. Fig. 15.에는 판과 보강재의 강종을 다르게 조합하여 하이브리드 보강판 시스템을 구성하여 보강재의 휨강성에 따른 면내극한강도를 비교하였다. 앞서 언급하였듯이 초기결함과 잔류응력이 극한강도산정에 모두 고려되었다. 보강되는 판의 종류에 따라 다양한 보강재 조합을 Fig. 15.에서 확인할 수 있다.
Fig. 15.를 통해서 강도(strength)가 높은 강재를 사용한 경우 낮은 강재를 사용한 경우보다 극한강도가 상당한 수준으로 향상되는 것이 확인되었다. 비교를 위해 탄성좌굴강도를 함께 표시하였는데, 탄성좌굴강도의 경우 강도(strength)와는 상관없이 강성(stiffness)에만 의존하므로 강재가 달라도 형상이 동일하면 같은 강도를 나타내고, 일정 이상의 보강재 강성을 확보되면 탄성좌굴강도는 더 이상 증가하지 않고 일정 강도를 유지하는 것을 알 수 있다. 비탄성극한강도의 경우, 보강재의 휨강성이 증가할수록 극한압축강도의 증가가 일부 나타나는데 강재의 강도가 높을수록 이 효과가 뚜렷함을 알 수 있다. 강재의 강도(strength)대비 보강판의 극한압축강도를 비교하면 HSB690판의 극한압축강도는 HSB460판 및 SM355판 대비 각각 26% 및 58% 수준으로 증가된 값을 보였다. 가격 등이 고려된 경제성평가가 있어야겠지만 고강도 강재 보강판 시스템의 경제성이 입증될 수 있다는 가능성이 충분하다고 보여진다. 또한 판(plate)과 보강재(stiffener)로 구성되는 보강판 시스템에서 극한강도는 높은 강도의 판을 사용하면 낮은 강도의 보강재를 사용해도 극한강도의 차이는 미세하게 나타난다는 것을 확인할 수 있다. 그러므로 판형 보강재를 사용한 하이브리드 보강판에서 보강재의 강재 선택 시 강성이 낮은 강재를 사용함으로써 비용절감 효과를 기대할 수 있다.
6. 결론
본 연구에 적용한 수치를 바탕으로 판형 보강재로 보강된 보강판 시스템의 극한거동을 알아보기 위해 범용 구조해석 프로그램인 ABAQUS를 이용하여 선형/탄성해석, 비선형/비탄성 해석이 수행되었다. 일반 강재인 SM355강재로 보강된 보강판 시스템의 면내력에 저항하는 거동을 초기결함과 잔류응력을 모두 고려하여 면내 극한강도를 평가하였다. 잔류응력은 보강판 설계시 무시해서는 안되는 주요매개변수로써 안전측면에서 설계시 반드시 고려해야 할 것으로 판단된다.
보강재의 세장비(h/ts) 변화에 따른 보강판시스템의 극한압축강도의 분포 분석을 통해, 세장비가 20 이하의 범위에서 휨강성이 증가하면 압축강도는 향상된다는 것을 확인할 수 있었다. 현행 설계기준인 KDS 14 31 10 강구조부재설계기준(한계상태설계법))에서 보강재의 돌출폭-두께비 제한값은 일반강재 기준으로 11.5으로 산정되는데 본 해석연구에 의한 값 20과 비교해 보면 상당히 보수적으로 제한하고 있음을 알 수 있다.
판(plate)과 보강재(stiffener)에 일반강재와 고강도강재를 혼합 구성한 하이브리드 보강판의 비탄성극한강도해석 결과 극한강도는 보강재의 강종에 크게 영향을 받지 않고 보강되는 판의 강종에 의해 결정되는 것으로 확인되었다. 하이브리드 보강판 시스템에서 극한강도는 높은 강도의 판을 사용하면 낮은 강도의 보강재를 사용해도 극한강도의 차이는 미세하므로 하이브리드 보강판에서 보강재의 강재 선택 시 강성이 낮은 강재를 사용함으로써 비용절감 효과를 기대할 수 있다.
Acknowledgments
이 논문은 2016-2018학년도에 청주대학교 산업과학연구소가 지원한 학술연구조성비(특별연구과제)에 의해 연구되었음.
References
-
Mukhopadhyay, M., and Mukherjee, A. (1990) Finite Element Buckling Analysis of Stiffened Plates, Computers & Structures, Elsevier, Vol.34, No.6, pp.795-803.
[https://doi.org/10.1016/0045-7949(90)90350-B]

-
Yoo, C.H., Choi, B.H., and Ford, E.M. (2001) Stiffness Requirements for Longitudinally Stiffened Box-Girder Flanges, Journal of Structural Engineering, ASCE, Vol.127, No.6, pp.705-711.
[https://doi.org/10.1061/(ASCE)0733-9445(2001)127:6(705)]

-
Thang, D.D., Koo, M.-S., Hameed, A., and Jeong, Y.-D. (2009) Stiffness Requirement for Flat-Bar Longitudinal Stiffener of Box-Girder Compression Flanges, International Journal of Steel Structures, KSSC, Vol.9, No.2, pp.115-122.
[https://doi.org/10.1007/BF03249486]

- Dassault Systèmes Simulia Corp. (2014) Abaqus Analysis User’s Manual, Ver. 6.14, DSS, USA.
- Timoshenco, S., and Gere, J.M. (1961) Theory of Elastic Stability, McGraw-Hill, USA.
-
Szilard, R. (1974) Theory and Analysis of Plates: Classical and Numerical Methods, Prentice Hall, USA.
[https://doi.org/10.1115/1.3423469]

-
국가건설기준센터(2017) 강교설계기준(한계상태설계법, KDS 24 14 31).
Korea Construction Standards Center (2017) Design Standard of Steel Bridge (Limit State Design, KDS 24 14 31), Korea (in Korean). -
국가건설기준센터(2016) 강교설계기준(한계상태설계법, KDS 14 31 10).
Korea Construction Standards Center (2016) Design Standard of Steel Bridge (Limit State Design, KDS 14 31 10), Korea (in Korean). -
Shin, D.K., Le, V.A., and Kim, K. (2013) In-Plane Ultimate Compressive Strengths of HPS Deck Panel System Stiffened with U-Shaped Ribs, Thin-Walled Structures, Elsevier, Vol.63, No.2, pp.70-81.
[https://doi.org/10.1016/j.tws.2012.10.001]

-
Shin, D.K., Dat, B.V., and Kim, K. (2014) Compressive Strength of HPS Box Girder Flanges Stiffened with Open Ribs, Journal of Constructional Steel Research, Elsevier, Vol.95, No.4, pp.230-241.
[https://doi.org/10.1016/j.jcsr.2013.12.014]

-
윤동용, 김경식(2007) 수평보강재가 설치된 플레이트 거더의 휨 연성에 관한 연구, 한국강구조학회논문집, 한국강구조학회, 제19권, 제6호, pp.643-653.
Yoon, D.Y., and Kim, K.S. (2007) A Study on Flexural Ductility of Longitudinally Stiffened Plate Girders, Journal of Korean Society of Steel Construction, KSSC, Vol.19, No.6, pp.643-653 (in Korean). -
김경식(2013) 보강판시스템에 적용되는 판형보강재의 국부 좌굴거동, 한국산학기술학회논문지, 한국산학기술학회, 제14권, 제12호, pp.6521-6526.
Kim, K.-S. (2013) Local Buckling Behaviors of Flat-Type Stiffeners in Stiffened Plate System, Journal of the Korea Academia-Industrial cooperation Society, KAIS, Vol.14, No.12, pp.6521-6526 (in Korean). [ https://doi.org/10.5762/KAIS.2013.14.12.6521 ]