대골형 파형강판의 보강형태에 따른 휨강도 평가 실험 연구
Copyright ⓒ 2018 by Korean Society of Steel Construction
초록
SS315 강재를 사용한 대골형 파형강판의 보강 형태 별 휨강도를 평가하기 위한 실험연구를 수행하였다. 단일 강판과 네 종류의 보강 방식을 고려하였다. 리브 보강 강판의 경우 볼트 간격, 샌드위치 보강 강판의 경우 체결 볼트 개수, 리브 보강 일반 콘크리트 충전 강판의 경우 스터드 유무 및 간격을 달리하여 휨강도 실험을 실시하였다. 단일 강판의 휨강도와 비교하여 리브 보강 강판과 샌드위치 보강 강판은 각각 약 2.0배와 1.9배의 휨강도 증가를 확인하였다. 콘크리트를 충전한 리브 보강 강판의 경우 스터드의 유무 또는 스터드 간격 그리고 콘크리트의 강도가 휨강도에 미치는 영향은 제한적인 것을 확인하였고, 단일 강판의 휨강도 대비 약 3.7배의 휨강도 증가를 확인하였다.
Abstract
Experimental study was conducted to verify the flexural strength of deep corrugated steel beam using SS315 steel for various types of reinforcement. Single corrugated plate and four types of reinforcements were considered. For rib or sandwich reinforced corrugated plates, effect of bolt spacing or number of connection bolts were minor. Flexural strength of rib and sandwich reinforced corrugated plate were about two times higher than the flexural strength of single corrugated plate. For concrete-filled rib reinforce corrugated plates, effect of stud spacing and the compressive strength of concrete was negligible. Flexural strength of the concrete-filled rib reinforced corrugated plates was about 3.7 times higher than that of single corrugated plate.
Keywords:
deep corrugated steel plate, flexural strength, experimental study, steel structure, reinforcement키워드:
대골형 파형강판, 휨강도, 실험연구, 강구조, 보강1. 서 론
파형강판은 골을 성형하여 내하력을 갖게 한 연성관으로서 하중 및 반력이 관 둘레에 균등하게 분포되어 내하력이 크다. 따라서 같은 관경의 흉관 및 콘크리트 박스에 비하여 두께가 약 1/20∼1/40 정도이며, 중량도 약 1/5∼1/10 정도이다. 또한 여러 겹을 겹칠 수 있으므로 좁은 공간에서도 보관과 운반이 가능하다. 콘크리트 교량은 철거 시 폐기물로 분류되는 반면 파형강판 교량은 철거 후 재활용이 가능하여 친환경적이다. 공사비도 지간에 따라 약간 달라지지만 약 10∼20% 가량 절감이 가능하여 경제적으로도 유리하다. 그러나 아직 명확한 세부설계기준이 마련돼 있지 않아 파형강판을 이용한 시설물 공사로 인한 붕괴사고와 하자가 속출하고 있어 이에 대한 개선이 시급하게 요구되고 있다.
Hwang et al.(2004)[1]은 파형강판의 파형방향 인장실험을 통하여 국내 생산중인 표준형과 대골형 파형강판의 인장실험을 통하여 파형강판 구조물의 설계 시 필요한 두께별 항복응력을 정리하였으며, 또한 파형방향으로의 단위 골당 항복하중과 강성 등을 제안하였다. Lee(2004)[2]는 이음부가 있는 실험체와 없는 실험체에 대하여 파형강판 박스 컬버트 구조물 단면에 대한 휨강도 실험을 통해 파형강판의 이음부 유·무에 따른 휨강도를 평가하였다. 실험 결과 이음부 유·무에따라 휨강도가 약 20%의 차이를 나타내었으며, 이 휨강도는 실무에서 적용되는 박스 컬버트 설계기준인 강재 항복강도 300 MPa를 적용시켰을 때의 저항모멘트 보다 큰 값으로 파형강판을 이용한 박스 컬버트 단면에서의 이음부 위치에 대한 검토가 필요 없는 것으로 평가하였다. Choi(2005)[3]은 SS490 (현 KS 기준 SS315) 표준형과 SS540 (현 KS 기준 SS450) 대골형 실험체에 대해 각 두께 별로 이음부 압축강도를 산정하였고 평평한 강판부재, 강판부재의 이음부, 곡률이 급격히 변화하는 헌치부 강판의 휨강도를 평가하였다. 실험결과 곡률반경이 급격히 변하는 헌치부 강판의 극한 모멘트는 이음부가 없는 평평한 경우의 50% 수준으로 나타나 헌치부에서는 휨성능이 저하 된다는 것을 확인할 수 있었다. 그러나 이는 ASTM(2003)[4]의 헌치부 모멘트 강도에 비하여 1.3배 가량 큰값으로 ASTM(2003)[4]의 헌치부 모멘트 강도를 이용하여 설계하는데 무리가 없는 것으로 판단하였다. Hwang(2009)[5]은 대골형 파형강판 단면을 개선하기 위하여 내부 굽힘각, 굽힘 반지름과 직선구간 길이와 같은 설계변수와 두께, 외부 굽힘각, 성형 전 강판의 폭, 성형 전 강판의 폭과 성형후 강판의 폭의 비의 설계상수와 구조적 제약조건을 고려하여 파형강판 단면 최적설계를 하였다.
국가설계기준 KDS 14 31 10 : 2016 강구조 부재 설계기준(하중저항계수설계법)[6]에 따르면 파형강판 구조물의 내하력을 증대시키기 위해 구조물을 보강할 수 있도록 허용하고 있다. 강재를 이용해 보강한 경우에는 휨에 대한 단면계수를 원단면과 보강단면의 휨에 대한 단면계수를 더한 값을 사용하도록 하고, 원단면과 보강단면으로 폐합된 내부에 콘크리트를 충전한 경우에는 콘크리트 단면을 제외한 원단면과 보강단면의 합성단면에 대한 휨에 대한 단면계수를 사용하도록 하고 있다. 단, 콘크리트 합성효과가 실험으로 입증될 때에는 휨에 대한 단면계수에 콘크리트 합성효과를 포함할 수 있도록 허용하고 있다.
ASTM A761/A761M[7]에 따르면 파형으로 절곡하기 전 파형강판의 최소 항복강도는 일반형은 190 MPa, 대골형은 275 MPa를 만족해야한다. 파형으로 절곡한 후에는 항복응력이 증가하여 대골형 파형강판의 경우에는 설계 항복응력으로 300 MPa를 제시한다. 이 규정은 AASHTO LRFD Bridge Design Specifications[8], CHBDC[9], AISI[10] 등 북미에서 사용하고 있는 모든 파형강판 구조물 설계기준들의 재료 규정으로 사용되고 있다. ASTM A964/A964[11]은 보강을 실시한 파형강판에 대한 소성모멘트 강도를 제시하고 있다. 우리나라 설계기준과 마찬가지로 원단면과 보강한 단면의 소성모멘트 강도의 합을 사용하도록 하며 콘크리트를 충전한 경우에 대한 강도는 제시하지 않고 있다[12],[13].
본 연구는 SS315 소재를 사용한 대골형 파형강판에 대한 기계적 성질을 명확하게 정의하기 위한 보강 형태 별 휨강도를 산정하기 위한 휨실험을 통하여 보강 단면에 대한 극한모멘트 강도를 평가하였다.
2. 실험 개요
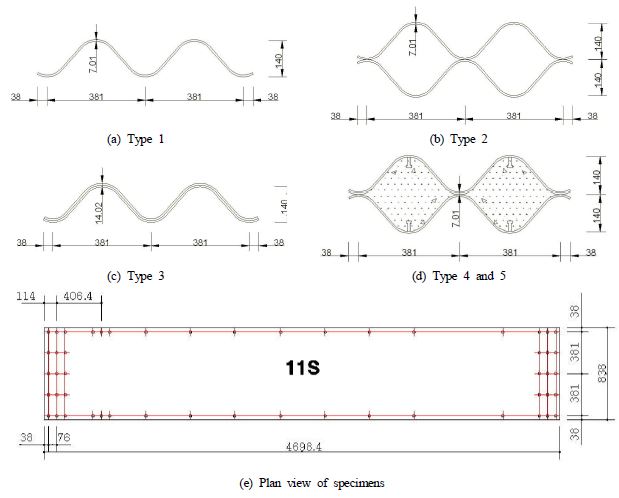
휨강도 실험을 위한 모든 시험체는 SS315 강재를 적용한 대골형 파형강판을 사용하였다. 파형강판의 두께는 7.01mm이고 골 간격 및 높이는 각각 381mm와 140mm이다.
2.1 시험체 종류
휨강도 실험에 사용된 시험체는 총 다섯 종류로 네 종류의 보강 단면과 단일 강판에 대한 휨강도 실험을 실시하였다. 보강 단면은 콘크리트를 충전하지 않은 경우 두 장의 파형강판의 골을 접합하여 폐합단면을 만든 리브 보강 단면(Type 2)과, 두 장의 파형강판을 겹친 샌드위치 보강 단면(Type 3)을 준비하였다. 볼트에 의한 파형강판 접합 효과를 확인하기 위해 각각 2 종류의 볼트 간격 또는 볼트 결합 개수를 적용하였다. 콘크리트를 충전한 경우에는 압축강도가 24 MPa인 일반 콘크리트를 사용한 Type 4와 압축강도가 40 MPa인 고강도 콘크리트를 사용한 Type 5를 준비하였다. 일반 콘크리트를 충전한 시험체를 이용하여 스터드 간격에 따른 합성효과를 확인하기 위해 스터드가 없는 경우와 스터드 간격이 다른 세 종류의 시험체를 준비하였다. 각 시험체의 단면 형상 및 제원은 Fig. 1.에 나타내었다. 모든 시험체는 F8T M20 볼트를 이용하여 체결하였다. 각 시험체 종류별로 3개의 시험체를 준비하였으며 총 30개의 시험체에 대한 휨강도 실험을 실시하였다. 각 시험체 종류 별 볼트 간격, 볼트 개수 및 스터드 간격은 Table 1에 제시되어있다.
각 시험체 Type 별 설계 휨강도를 Table 2에 제시하였다. 모두 KDS 14 31 10[6]에서 제시하는 규정에 따라 계산하였다. 리브 보강 강판(Type 2)과 샌드위치 보강 강판(Type 3)은 원단면과 보강단면을 각각 계산하여 합하였고, 콘크리트 충전 리브 보강 강판인 Type 4와 5는 콘크리트를 제외한 원단면과 보강단면이 완전 합성되었다고 가정하고 계산하였다.
3. 실험 결과
3.1 재료 시험
휨강도 실험에 앞서 시험체에 사용된 재료들의 강도를 확인하는 실험을 실시하였다. 파형강판의 인장시험 결과 평균 항복강도 442 MPa, 평균 인장강도 558 MPa, 평균 파단연신율 30.8%로 측정되었다. 이는 KS D 3503와 KS D 3506에서 제시하는 SS315강재의 최소 항복강도 315 MPa보다 40%이상, 최소 인장강도 490 MPa보다 14%이상 증가된 값으로 나타났다.
일반 콘크리트와 고강도 콘크리트 공시체에 대한 압축강도 시험결과 일반 콘크리트의 평균 압축강도는 32 MPa로 공칭압축강도인 24 MPa 대비 32% 큰 값을 나타냈고, 고강도 콘크리트의 평균 압축강도는 50 MPa로 공칭압축강도인 40 MPa 대비 25% 증가된 값을 나타내어 모두 KS 규격을 만족하였다.
3.2 단일 강판 (Type 1)
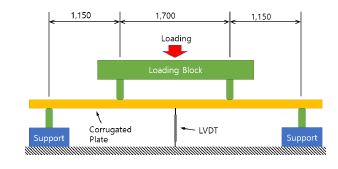
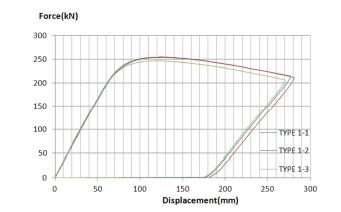
총 3개의 단일단면 실험체에 대한 휨실험을 통해 Fig. 3.과 같은 하중-중심부 처짐 곡선을 얻었다. 강판 중심부의 수직 변형량이 120~125mm일 때 극한하중에 도달하였다. Fig. 4.와 같이 3개의 실험체에서 동일하게 하중 재하부에서 국부좌굴이 발생하였다. 3개 실험체의 평균 극한하중은 242 kN이며, 이때의 평균 극한모멘트는 173 kN·m/m였다.
3.3 리브 보강 강판 (Type 2)
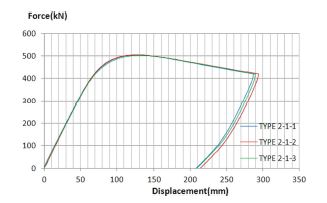
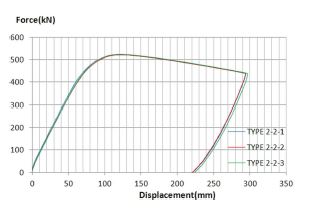
리브 보강 강판의 휨 실험은 2 종류의 볼트 간격을 적용하여 각각 3개의 실험체에 대해 실시하였다. Type 2-1 실험체의 하중-중심부 처짐 곡선은 Fig. 5.와 같다. Type 1과 마찬가지로 강판 중심부의 수직 변형량이 120~125mm일 때 극한하중에 도달하였으며, 이때의 평균 극한하중과 평균 극한모멘트는 각각 505 kN와 346 kN·m/m이었다. Type 2-2 시험체의 하중-중심부 처짐 곡선은 Fig. 6.과 같다. 강판 중심부의 수직 변형량이 120~125mm일 때 극한하중에 도달하였으며, 이때의 평균 극한하중은 523 kN, 평균 소성모멘트는 359 kN·m/m이었다. Type 1과 마찬가지로 모든 시험체의 하중 재하부에서 국부좌굴이 발생하였고 파괴 후 시험체의 형상은 Fig. 7.과 같다. Type 2-1과 2-2의 휨강도는 TYPE 2의 설계 휨강도인 250 kN·m/m보다 모두 약 1.4배 큰 것을 확인하였다.
3.4 샌드위치 보강 강판 (Type 3)
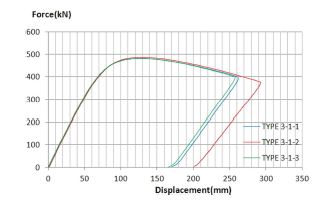
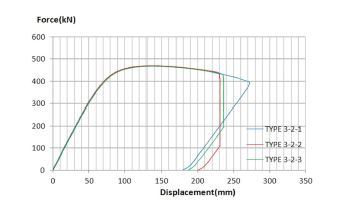
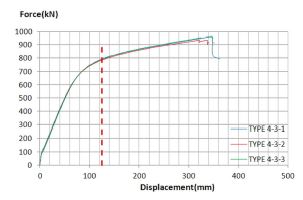
샌드위치 보강 강판의 휨실험은 두 종류의 볼트 결합 개수를 적용하여 각각 3개의 실험체에 대해 실시하였다. Type 3-1와 3-2 시험체의 하중-중심부 처짐 곡선은 각각 Fig. 8.과 9와 같다.
모두 중앙부 처짐이 약 120~125mm일 때 극한하중에 도달하였다. Type 3-1 시험체의 평균 극한하중은 약 484 kN이었으며 이때의 평균 극한모멘트는 약 332 kN·m/m이다. Type 3-2 시험체의 평균 극한하중은 약 469 kN이었으며 이때의 평균 극한모멘트는 약 322 kN·m/m이었다.
모든 Type 3 시험체는 Fig. 10.과 같이 시험체의 중앙에서 좌굴이 발생한 것을 확인하였다. Type 3는 두 장의 강판이 겹쳐져있어 하중 재하부에서 발생할 수 있는 국부좌굴에 대한 저항 강도가 더 크기 때문에 Type 1과 2와는 다르게 하중 재하부에서 국부좌굴이 발생하지 않은 것으로 보인다.
3.5 일반 콘크리트 충전 리브 보강 강판 (Type 4)
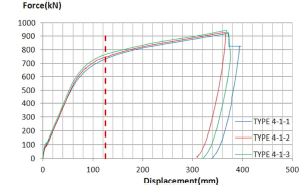
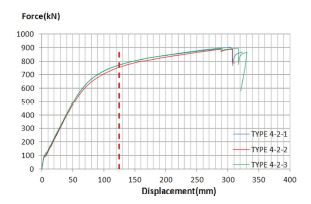
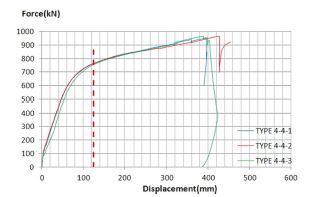
일반 콘크리트를 충전한 리브 보강 강판 시험체는 스터드 간격의 영향을 확인하기 위해 스터드가 없는 시험체와 스터드 간격이 406mm, 813mm, 1626mm인 네 종류의 시험체에 대해 각각 3개씩 실험을 실시하였다. Type 4-1부터 4-4 시험체들이 하중-중심부 처짐 곡선은 Fig. 11.~14.와 같다. 모든 시험체들은 Fig. 15.와 같이 시험체 끝단의 볼트가 파단되면서 극한하중에 도달하지 못하였다. 시험 종료 시 시험체의 변형 형상은 Type 2의 형상과 같았다. 콘크리트를 충전하지 않은 강판의 휨강도 실험 결과 모두 중심부 변위가 약 120~125mm일 때 극한하중에 도달하였다. 따라서 콘크리트가 충전된 시험체더라도 중심부 변위가 같은 값이면 강판이 항복했다는 것을 유추할 수 있다. 콘크리트를 충전하지 않은 시험체들과 동일한 조건에서 비교하기 위해 시험체의 중심부 변위가 123mm일 때의 하중과 모멘트를 강판 항복 하중 및 모멘트로 명명하였다. 시험체의 극한 하중 및 모멘트는 시험 중 확인한 최대 하중과 해당 하중에 대한 모멘트로 정의하였다.
Fig. 11.~14.에서 보는 바와 같이 동일한 스터드 간격을 가진 시험체는 모두 유사한 하중-중심부 처짐 곡선을 나타내었다. 중심부 변위가 123mm일때의 강판 항복 모멘트는 Table 3에 나타낸 바와 같이 스터드가 있는 경우 약간 더 큰 값을 보이나 스터드가 있는 경우의 최대값과 스터드가 없을 경우의 값의 차이는 약 5.7%에 불과하다. Type 4-1부터 4-4의 시험 결과를 평균한 경우 단일강판의 극한모멘트 대비 약 3.0배의 강도 증가를 확인했다. 볼트가 파단될 때의 하중으로 극한모멘트를 평가하면 평균 극한강도는 약 643 kN·m/m이고 스터드 간격에 따른 최대-최소 극한모멘트의 차이는 약 6.7%이었다.
3.6 고강도 콘크리트 충전 리브 보강 강판 (Type 5)
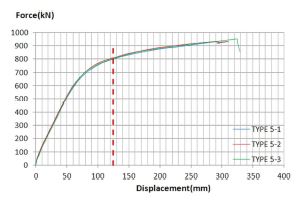
고강도 콘크리트를 충전한 리브 보강 강판 시험체는 813mm의 스터드 간격을 적용하였다. 모든 시험체에서 Type 4와 마찬가지로 단부의 볼트가 파단되어 실험이 종료되었으며 하중-중앙부 처짐 곡선은 Fig. 16.과 같다. Type 4와 마찬가지로 각 시험체의 강판 항복 모멘트는 중심부 처짐이 123 mm일 때의 하중으로 결정하였으며 평균 강판 항복 모멘트는 약 553 kN·m/m로서 단일 강판 대비 약 3.2배의 강도 증가가 확인되었다. 볼트가 파단될 때의 하중으로 극한모멘트를 평가하면 약 646 kN·m/m이었다. Type 4와 마찬가지로 시험 종료 시 시험체의 변형 형상은 Type 2와 같았다.
4. 보강 형태에 따른 휨강도 평가
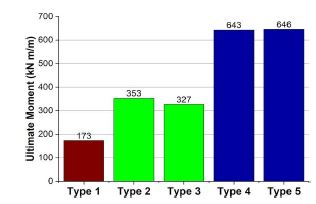
휨강도 평가 실험 결과를 Fig. 17.에 나타내었다. 각 보강 형태 별로 볼트의 간격, 볼트의 개수, 또는 스터드 간격의 차이를 주어 이들이 휨성능에 어떤 영향을 미치는지 확인하였으나 모두 휨강도에 미치는 영향이 미미하였다. 이러한 실험 결과를 반영하여 각 보강 형태별로 모든 시험체의 극한모멘트를 평균하였다.
먼저 콘크리트를 충전하지 않은 경우인 Type 2와 Type 3은 단일 강판의 극한모멘트인 Type 1보다 각각 2.0배와 1.9배 큰 값을 나타내었다. 이는 KDS 14 31 10[6]과 ASTM A964/964M(ASTM, 2017)[11]에서 휨에 대한 단면계수를 원단면과 보강한 단면의 휨에 대한 단면계수를 더한 값을 사용하도록 하는 것이 타당함을 보여준다. 단 샌드위치 보강을 한 Type 3의 경우 원단면과 보강한 단면이 같음에도 단일 강판의 극한모멘트의 2.0 배보다 약간 작은 값을 나타내었으나 일반적으로 소재의 실제 항복강도가 공칭 항복강도보다 큰 것을 감안하면 이 정도의 차이는 무시할 수 있다고 판단된다.
원단면과 보강단면으로 폐합된 내부에 콘크리트를 충전한 경우인 Type 4와 5의 경우 스터드 유무 또는 콘크리트의 강도에 따른 극한 모멘트의 차이를 확인할 수 없었다. 폐합단면에 콘크리트를 충전하여 보강하는 경우에 대한 설계 휨강도는 우리나라의 KDS 14 31 10[6]에만 제시되어있는데 이 경우 콘크리트를 제외하고 원단면과 보강단면이 완전 합성되었다고 가정하고 휨강도를 산정한다. 콘크리트 충전 없이 두 단면이 완전 합성되었다고 가정한 경우 설계휨강도는 단일 강판의 휨강도 대비 약 3.3배이다. 실험을 통해 확인한 극한모멘트는 단일 강판의 극한모멘트 대비 3.7배로서 설계기준에서 제시하는 휨강도를 상회한다. 따라서 콘크리트를 충전한 폐합 단면의 경우 강재의 단면이 완전 합성된 것으로 가정하는 설계기준은 적절한 것으로 판단된다.
5. 결 론
SS315 강재를 사용한 대골형 파형강판의 보강형태에 따른 휨강도 실험 결과 다음과 같은 결론을 얻을 수 있다.
리브 보강 강판은 단일 강판보다 휨강도가 약 2.0배 증가하는 것을 확인하였으며, 볼트 결합 간격을 절반으로 줄여 볼트 체결력을 2.0배 증가시켜도 휨강도 증가 정도가 미미한 것을 확인하였다. 샌드위치 보강 강판은 단일 강판 대비 휨강도가 1.9배 증가하였으며 볼트 결합 개수 증가에 따른 휨강도 변화는 무시할 수 있는 정도이었다. 콘크리트를 충전하지 않고 보강한 경우 현 설계기준에서 제시하는 바와 같이 원단면과 보강단면의 합성효과를 고려하지 않고 각각의 휨강도를 더하는 것이 타당함을 보여준다.
콘크리트를 충전한 리브 보강 강판의 경우 스터드의 유무 또는 콘크리트 강도에 따른 휨강도 변화가 약 7% 이내인 것을 확인하였다. 따라서 고강도 콘크리트를 사용하거나 스터드를 설치하는 것의 필요성이 충분하지 않다고 볼 수 있다. 실험 시 극한하중을 확인하지 못하였으므로 실험 시 확인한 최대 하중으로 휨강도를 평가할 경우 단일 강판의 휨강도 대비 약 3.7배가 되는 것을 확인하였다. 이는 현 설계기준에서 원단면과 보강단면의 합성효과를 고려하여 평가하는 경우 단일 강판의 휨강도 대비 3.3배의 휨강도를 산정하는 것이 타당함을 나타낸다.
Acknowledgments
본 연구에서의 실험은 청암건업과 명지대학교 하이브리드구조실험센터의 지원으로 이루어졌으며 감사드립니다.
References
-
황원섭, 강승표, 위영민(2004) 파형강판 이음부 강도 및 응력분포특성에 관한 연구, 한국강구조학회논문집, 한국강구조학회, 제16권, 제3호, pp.365-375.
Hwang, W.S., Kang, S.P., and Wi, Y.M. (2004) Strength and Stress Distribution Behavior for the Connections of Corrugated Steel Plates, Journal of Korean Society of Steel Construction, KSSC, Vol.16, No.3, pp.365-375 (in Korean). -
이경모(2004) 대골형 파형강판 휨강도에 대한 연구, 석사학위논문, 서울산업대학교.
Lee, K.M. (2004) A Study on Flexural Strength for Deep Corrugated Steel Plate, Master’s Thesis, Seoul National University of Science and Technology, Korea (in Korean). -
최문성(2005) 파형강판 구조물의 이음부 압축강도와 휨강도에 대한 평가, 석사학위논문, 한양대학교.
Choi, M.S. (2005) Evaluation of Compressive Seam Strength and Flexural Strength of Corrugated Structural Plates, Master’s Thesis, Hanyang University, Korea (in Korean). - American Society for Testing and Materials (2003) Standard Specification for Corrugated Steel Box Culverts (A964/A964M), USA.
-
황규태(2009) 파형강판 구조물의 최적단면 설계에 관한 연구, 석사학위논문, 한양대학교.
Hwang, K.T. (2009) A Study on Optimal Design of Corrugated Steel Plate Structures, Master’s Thesis, Hanyang University, Korea (in Korean). -
국가건설기준센터(2016) 강구조 부재 설계기준(하중저항계수설계법, KDS 14 31 10).
Korea Construction Standards Center (2016) Design Standards for Steel Member (Load and Resistance Factored Design, KDS 14 31 10), Korea (in Korean). - American Society for Testing and Materials (2018) Standard Specification for Corrugated Steel Structural Plate, Zinc-Coated, for Field Bolted Pipe, Pipe-Arches, and Arches (A761/A761M), USA.
- American Association of State Highway and Transportation Officials (2014) AASHTO LRFD Bridge Design Specifications (7th Ed.), USA.
- Standards Council of Canada (2006) Canadian Highway Bridge Design Code (CAN/CSA-S6-06), Canada.
- American Iron and Steel Institute (2002) Cold-Formed Steel Design Manual, AISI, USA.
- American Society for Testing and Materials (2017) Standard Specification for Corrugated Steel Box Culverts (A964/A964M), USA.
-
문성환, 오상훈(2015) 원형 파형강판의 전단 및 휨 성능평가에 관한 연구: 전단 및 휨강도 설계식 제안, 한국강구조학회논문집, 한국강구조학회, 제27권, 제5호, pp.455-470.
Moon, S.H., and Oh, S.H. (2015) A Study on Shear and Flexural Performance Evaluation of Circularly Corrugated Plate, Journal of Korean Society of Steel Construction, KSSC, Vol.27, No.5, pp.455-470 (in Korean). [ https://doi.org/10.7781/kjoss.2015.27.5.455 ]
-
문지호, 이종원, 최병호, 이학은(2007) 균일한 휨모멘트가 작용하는 파형강판 복부판 I-거더의 횡-비틂 좌굴강도 평가, 한국강구조학회논문집, 한국강구조학회, 제19권, 제5호, pp.463-472.
Moon, J.H., Yi, J.W., Choi, B.H., and Lee, H.E. (2007) Evaluation of Lateral-Torsional Buckling Strength of I-Girder with Corrugated Web Under Uniform Bending, Journal of Korean Society of Steel Construction, KSSC, Vol.19, No.5, pp.463-472 (in Korean).